Centre analytique
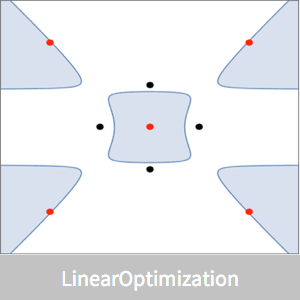
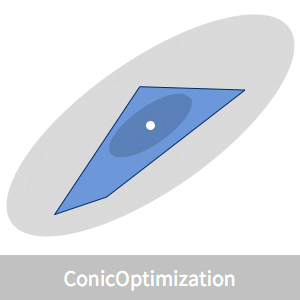
Un polygone convexe peut être représenté par des intersections de demi-plans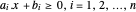 
. Le centre analytique peut être défini comme un point, situé à l'intérieur du polygone, qui maximise le produit des distances sur les côtés. La distance d'un point 
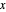dans le polyèdre dont chaque côté correspond à 
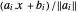. Par conséquent, le centre analytique correspond à 
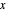, ce qui augmente la valeur de 
.
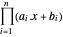Cet exemple démontre comment les contraintes du cône exponentiel peuvent être utilisées avec ConicOptimization pour trouver le centre analytique, ainsi que de la façon dont la représentation des inégalités pour un polygone peut être extraite en utilisant LinearOptimization.
Prenons un polygone convexe.
Extrayez les coefficients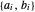 
de chaque côté.
Les inégalités scalaires correspondant au polygone sont :
Pour exprimer le problème sous la forme d'une minimisation convexe, considérez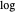 
et inversez l'objectif 
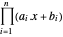. L'objectif transformé est 
.
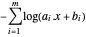Puisqu'une somme de logarithmes est concave, la négation est convexe, et par conséquent une variable auxiliaire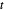 
peut être introduite comme fonction-objectif avec 
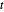sous la contrainte 
.
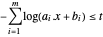Visualisez l'emplacement du centre analytique.
Il existe des formules simples qui fournissent des ellipsoïdes inscrits et des ellipsoïdes de recouvrement qui se concentrent sur le centre analytique.
