Minimal begrenzendes Ellipsoid
Ermitteln Sie das Löwner-John-Ellipsoid bei einer Menge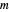 
von Punkten 
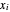in 
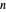Dimensionen. Es handelt sich dabei um das minimal begrenzende Ellipsoid, das eine vorgegebene kompakte Menge enthält.
Dieses Beispiel zeigt, dass NMinimize bei Problemen, die in Form von hochgradig nichtlinearen konvexen Zielfunktionen und -beschränkungen ausgedrückt werden, Transformationen durchführen kann, mit denen das Problem durch konvexe Optimierung leicht gelöst werden kann.
Ein Ellipsoid in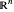 
kann durch Punktemenge 
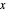so beschrieben werden, dass 
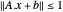, wobei 
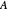eine positive semidefinite 
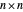Matrix und 
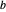ein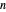 
-Vektor ist. Das Volumen des Ellipsoids ist proportional zu 
. 
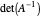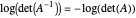ist konvex. Gefragt ist die Lösung von
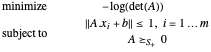
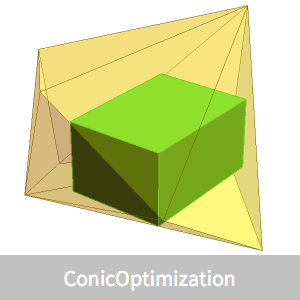
Das hier gezeigte Beispiel bezieht sich auf eine zufällige Menge von Punkten in drei Dimensionen, so dass eine Visualisierung möglich ist. Der Lösungsalgorithmus kann jedoch auch mit größeren Dimensionen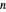 
arbeiten.
Finden Sie mit NMinimize die Lösung.
In drei Dimensionen kann das Ellipsoid mithilfe der Ellipsoid-Graphikprimitive beschrieben werden.
BoundingRegion kann ein begrenzendes Ellipsoid schneller finden, aber das Volumen ist größer.
