最小包囲楕円体
次元において 
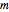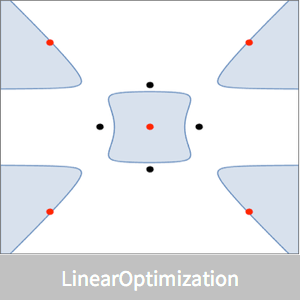
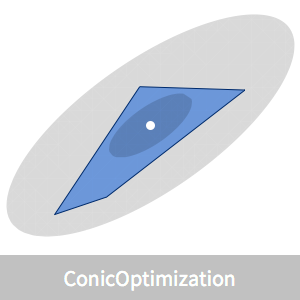
個の点の集合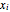 
が与えられたとき，すべての点を囲む最小体積楕円体であるLöwner-John楕円体を求める．
この例題では，高非線形の凸目的関数および制約条件で表される問題の場合，NMinimizeを使うと凸最適化で簡単に解ける問題に変換できることを示す．
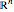の楕円体は，
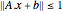である点集合 
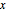によって記述することができる．このとき 
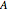は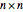 
の半正定値行列，
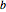は 
ベクトルである．楕円体の体積は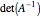
に比例する．
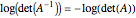は凸であり，以下の解を見付ける．
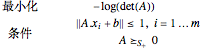
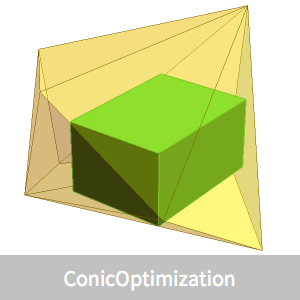
ここで示す例題は，可視化ができるように三次元のランダムな点集合で行われた．解のアルゴリズムはより大きい次元 
を扱うことができる．
NMinimizeを使って解を求める．
三次元では，楕円体はEllipsoidグラフィックスプリミティブで記述することができる．
BoundingRegionは包囲する楕円体をより速く求めることができるが，その楕円体の体積は大きくなる．
