Problema de optimización estructural
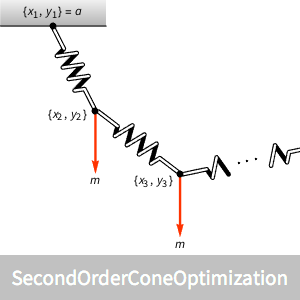
Encuentre la forma de una cadena colgante formada por varios enlaces de resortes, con una masa en cada unión de enlace.
Este ejemplo demuestra cómo una condición de energía mínima para el equilibrio puede ser expresada en términos de un problema de optimización con restricciones cónicas (norma) de segundo orden que puede ser fácilmente resuelto con SecondOrderConeOptimization.
Encuentre la forma de una cadena colgante formada por 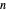 enlaces de resorte bajo una carga vertical al final de cada enlace. El objetivo es encontrar las posiciones de enlace
enlaces de resorte bajo una carga vertical al final de cada enlace. El objetivo es encontrar las posiciones de enlace 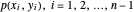 dadas las posiciones en los extremos
dadas las posiciones en los extremos 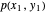 y
y 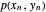 .
.
La energía potencial debido a la gravedad, ignorando el peso de los resortes, es 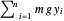 , donde
, donde 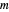 es la carga vertical en cada extremo y
es la carga vertical en cada extremo y 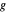 es la gravedad estándar.
es la gravedad estándar.
La energía potencial debido a la tensión en el enlace de resorte causada por estiramiento es 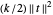 , donde
, donde 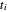 es el estiramiento en el enlace de resorte
es el estiramiento en el enlace de resorte 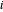 y
y 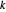 es la rigidez del resorte. Usando
es la rigidez del resorte. Usando 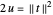 , la energía se transforma a
, la energía se transforma a 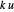 .
.
Una restricción adicional 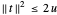 debe ser agregada debido a la transformación.
debe ser agregada debido a la transformación.
Los extremos de la cadena enlazada se sujetan en las posiciones 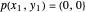 y
y 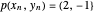 .
.
Debido a que  es convexa, es suficiente para requerir que cada resorte cumpla con la condición
es convexa, es suficiente para requerir que cada resorte cumpla con la condición 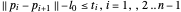 , donde
, donde 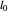 es la longitud de descanso de cada resorte.
es la longitud de descanso de cada resorte.
Los parámetros de diseño se muestran a continuación.
La función objetivo final es la suma de la gravedad y la energía potencial del resorte que debe ser minimizada.
Encuentre los extremos de cada uno de enlaces de resorte.
Visualice la forma de la cadena de resorte resultante.
El tramo es mayor para los enlaces cercanos a los extremos de la cadena de enlaces. Los enlaces 11 y 12 tienen la menor elongación.
La solución es lo suficientemente rápida para manipular el número de enlaces y extremos.