Optimización de trayectoria

Minimice 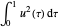sujeto a .

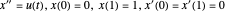Este ejemplo demuestra cómo un problema variacional puede ser discretizado a un problema de optimización finito resuelto eficientemente mediante métodos convexos, tales como QuadraticOptimization.

El problema variacional será aproximado discretizando el problema de valor límite y usando la regla trapezoidal para integrar en una retícula espaciada uniformemente en el intervalo [0,1], 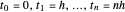con .

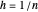Permita que la variable u[i] represente 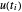y x[i] represente 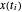para .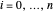

La restricción de la ecuación diferencial es fácilmente representada usando aproximaciones de diferencia de segundo orden centradas para 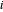desde 1 a .

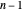En el límite, las condiciones de derivación cero permiten el uso de puntos ficticios 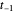y 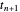. Cuando 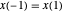y 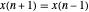, la fórmula de diferencia de segundo orden para la primera derivada 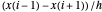es cero para 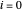y 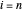. Entonces, en el límite, use lo siguiente.

La regla trapezoidal para 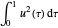es proporcionada por lo siguiente.

Dado que la expresión de la regla trapezoidal es cuadrática y todas las restricciones son de igualdad lineal, el mínimo de la integral discretizada puede ser encontrado usando QuadraticOptimization directamente.

Las funciones aproximadas son construidas con Interpolation.

Una solución analítica exacta, 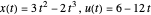, es conocida para este problema, así que es posible graficar el error en la discretización.

El error asintótico es aproximadamente 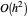, así que al duplicar 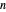a 200 y recalcular, el error será alrededor de 1/4 de lo que se muestra aquí.

La solución analítica puede ser encontrada considerando una familia de curvas 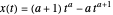donde 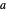es un parámetro. Esta curva paramétrica cumple con las condiciones de límite prescritas 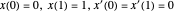. Dado que 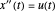, se puede encontrar un parámetro óptimo 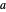que minimice .

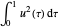El valor óptimo de 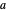está en 2, que es el resultado analítico .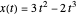