Problema de corte máximo
El problema de corte máximo determina un subconjunto 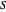 de los vértices
de los vértices 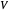 de un grafo, para el cual se maximiza la suma de los pesos
de un grafo, para el cual se maximiza la suma de los pesos 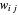 de los bordes que cruzan desde
de los bordes que cruzan desde 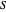 a su complemento
a su complemento 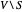 .
.
Este ejemplo demuestra cómo SemidefiniteOptimization puede ser usada para configurar una función que resuelva eficientemente una relajación del problema de corte máximo completo NP.
Asuma que 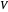 tiene
tiene 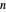 vértices de modo que pueden ser descritos por un índice
vértices de modo que pueden ser descritos por un índice 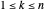 . Permita que
. Permita que 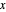 sea un vector con componentes
sea un vector con componentes 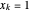 para
para 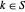 y
y 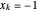 para
para 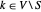 con tal que
con tal que 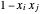 sea distinto de cero (=2) solo si
sea distinto de cero (=2) solo si 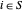 y
y 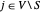 . Entonces el corte máximo se encuentra maximizando
. Entonces el corte máximo se encuentra maximizando 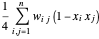 , donde
, donde 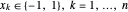 . El objetivo puede ser rescrito como:
. El objetivo puede ser rescrito como:
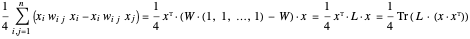
... donde 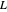 es la matriz laplaciana del grafo y
es la matriz laplaciana del grafo y 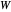 es la matriz de adyacencia ponderada.
es la matriz de adyacencia ponderada.
Para casos más pequeños, el problema de corte máximo puede ser resuelto exactamente, pero no es práctico para grafos más grandes dado que en general el problema posee complejidad NP completa.
El problema minimiza 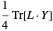 , donde
, donde 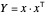 es una matriz semidefinida positiva de rango simétrico-1, con
es una matriz semidefinida positiva de rango simétrico-1, con 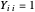 para cada
para cada 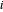 , equivalente a
, equivalente a 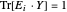 , donde
, donde 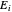 es la matriz con
es la matriz con  en la posición diagonal
en la posición diagonal 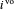 y 0 en las demás posiciones.
y 0 en las demás posiciones.
Para hacer que la solución sea práctica, resuelva un problema relajado donde la condición de rango-1 es eliminada de manera que solo requiera 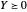 .
.
El problema semidefinitivo en forma dual es proporcionado por
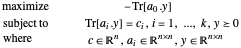
Y se resuelve usando SemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }].
Para la solución 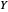 del problema relajado, se construye un corte mediante el redondeo aleatorio: descomponga
del problema relajado, se construye un corte mediante el redondeo aleatorio: descomponga 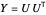 , permita que
, permita que 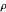 sea un vector aleatorio de la norma de la unidad distribuido uniformemente, y permita que
sea un vector aleatorio de la norma de la unidad distribuido uniformemente, y permita que 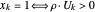 . Para demostración, se define una función que demuestra el valor relajado, el valor redondeado y el grafo, con los vértices en
. Para demostración, se define una función que demuestra el valor relajado, el valor redondeado y el grafo, con los vértices en 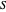 mostrados en rojo.
mostrados en rojo.
Encuentre un corte máximo aproximado usando el procedimiento demostrado anteriormente, y compare con el resultado exacto.
Encuentre el corte máximo para un grafo de retícula.
Encuentre el corte máximo para un grafo aleatorio.
Compare los tiempos para los algoritmos relajados y exactos para un grafo de Peterson.