Suavizado para preservación de estructuras
La regularización de ajuste de variación total se puede utilizar para filtrar el ruido en una señal y al mismo tiempo preservar los saltos significativos.
Este ejemplo demuestra cómo el modelado directo en términos de las funciones de Wolfram Language puede ser usado para implementar la regularización de ajuste de variación total de forma natural utilizando NArgMin.
Para una señal 
, esto puede hacerse encontrando los valores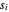 
que minimicen 
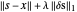, donde 
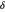s es el vector con elementos 
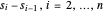y λ es un parámetro que se utiliza para compensar entre la reducción del ruido y la proximidad a la señal 
.
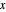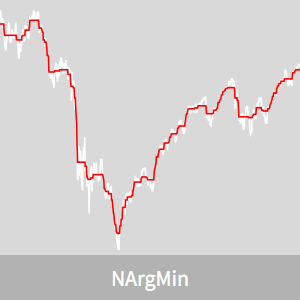
Considere el índice bursátil industrial promedio de Dow Jones durante la crisis financiera del 2008. Hay mucha volatilidad cotidiana que a largo plazo puede considerarse efectivamente como ruido.
La señal es la secuencia de valores del índice bursátil.
Encuentre el índice de suavizado para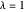 
. Method->"Convex" es usado ya que otros métodos serían muy lentos, aún si lograran ser exitosos para tantas variables.
Compare el índice suavizado con el índice actual.
El índice suavizado muestra las tendencias principales pero omite algunas características importantes. Existe una compensación entre las características de captura y el grado de suavizado que se realiza, y es determinado por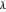 
. Para 
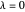, no hay suavizado y 
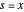. Por otro lado, en tanto 
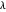se acerca a ∞, 
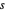se acercará a una señal constante. Un gráfico de la variación total versus la desviación de la señal original para valores distintos de 
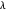puede dar una indicación de valores apropiados de 
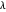para lograr el mejor equilibrio.
Existe una curvatura notable en la curva alrededor de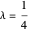 
, indicando que esto logra un equilibrio razonable.
Es interesante ver el índice suavizado para algunos de los distintos valores de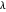 
.
La minimización también puede ser pensada en términos de un ajuste de mínimos cuadrados con la regularización. La nueva opción FitRegularization puede ser usada en Fit para hacer esto.
