Calculez l'invariant de Klein pour une courbe elliptique
Les invariants des fonctions elliptiques de Weierstrass sont des concepts standard définis pour les courbes elliptiques. La version 12 fournit des fonctions pour travailler directement avec ces invariants, ainsi que les demi-périodes et les valeurs à demi-périodes de ces fonctions elliptiques.
WeierstrassE1, WeierstrassE2 et WeierstrassE3 donnent les valeurs de WeierstrassP aux demi-périodes correspondantes.
De la même manière, WeierstrassEta1, WeierstrassEta2 et WeierstrassEta3 donnent les valeurs de WeierstrassZeta aux demi-périodes correspondantes.
Finalement, WeierstrassInvariantG2 et WeierstrassInvariantG3 définissent les invariants des fonctions elliptiques de Weierstrass, ce qui facilite leur utilisation dans des exemples comme celui qui suit. Définissez le discriminant de la courbe elliptique de Weierstrass.
Calculez le j-invariant de Klein en utilisant les g-invariants de la courbe.
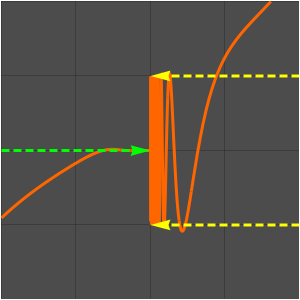
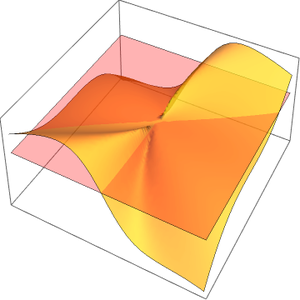
Représentez graphiquement la partie imaginaire de l'invariant de Klein.
Comparez avec la valeur de fonction intégrée.