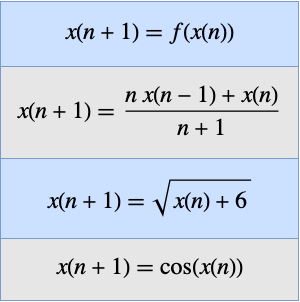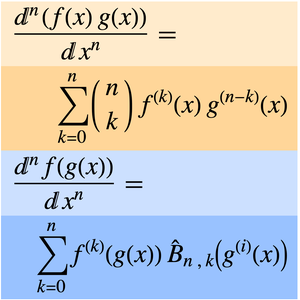Déterminez la limite d'une séquence
Les limites des séquences surviennent fréquemment dans les calculs infinitésimaux et peuvent exister même si les limites de fonction correspondantes n'existent pas. La fonction DiscreteLimit de la version 12 peut être utilisée pour calculer les limites de séquences données sous forme fermée ou spécifiées par des opérateurs formels, comme l'illustrent les exemples suivants.
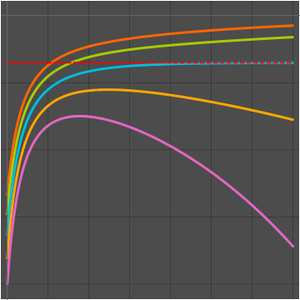
Déterminez la limite d'une séquence.
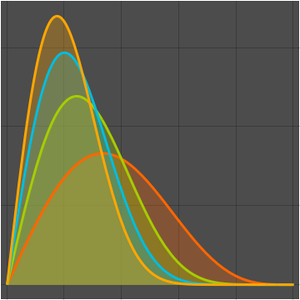
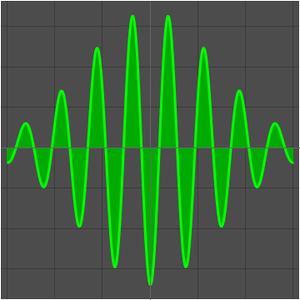
Visualisez la séquence.
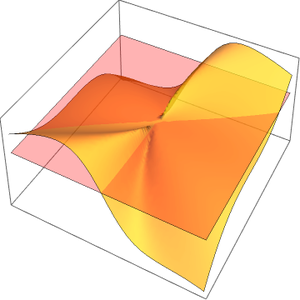
Déterminez la limite d'une séquence multivariée.
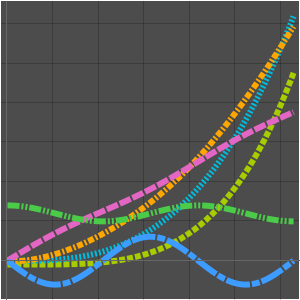
Visualisez la séquence.
L'exemple suivant utilise la règle de Stolz-Cesàro, une version discrète de la règle des limites de L'Hôpital, pour calculer la limite d'une somme Inactive imbriquée.
Déterminez la limite d'une fraction continue Inactive.
L'exemple suivant démontre qu'une limite de fonction peut ne pas exister, mais que la limite de séquence correspondante existe.
Définissez une fonction trigonométrique.
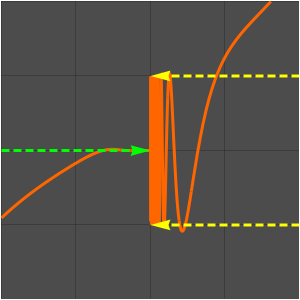
Représentez graphiquement la fonction et la séquence obtenue en échantillonnant la fonction sur des entiers.
La limite de fonction n'existe pas ici.
En effet, les valeurs de fonction oscillent entre -1 et 1.
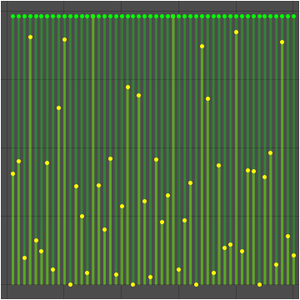
Cependant, la limite de séquence existe.
En effet, la séquence est constante à tous les points d'échantillonnage.