格子充填の密度を計算する
"Lattice"実体領域は，古典的な名前が付いた格子についての有益な情報を含んでいる．
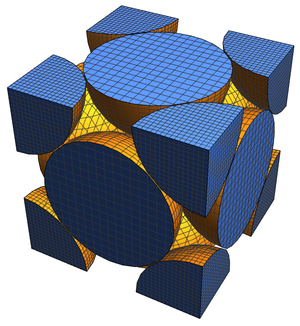
例として，"Image"特性を使って即座に可視化できる体心立方(BCC)格子について考えて見る．
格子充填の重要な特性は，適切な配置で充填された球によって占められる空間の割合である．体心立方格子の場合，この充填密度は以下で与えられる．
言い換えれば，球は体心立方充填の空間全体の約68%を占める．
この格子を生成する最小ベクトルは"MinimalVectors" 特性として入手可能である．
これらを使って空間充填の可視化が作成でき，そこから直接密度が計算できる．単位格子内に現れる球の中心を与えるリストを最小ベクトルから構築することから始める．
次に，プロット範囲を単位格子の領域に制限する．
中空の球体の代りに充填された球体を使って可視化をより精巧にすることができる．
この図から分かるように，単位格子の中には8分の1の球が8個と完全な球が1つあり，合せて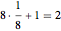
個の完全な球があることになる．球の半径を 
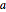とすると，ピタゴラスの定理を空間対角線に適用して，立方体全体の辺の長さは
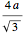になる．これは球の充填密度がすでに見た式で与えらることを意味する．
次に，面心立方体(FCC)格子について考えてみよう．
この格子充填の方が充填密度が高い．
つまり，球が面心立方格子充填の全空間の約74%を占める．
前と同じように，面心立方格子充填における球の中心を求めることで，空間充填の可視化を作成する．
この図から分かるように，単位格子内には8分の1の球が8個に半分の球が6個あり，全体で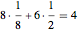
個の完全な球があることになる．球の半径を 
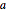とすると，ピタゴラスの定理を面の対角線に適用して，立方体全体の辺の長さは
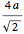になる．これは球の充填密度がすでに得られた式で与えらることを意味する．
六方最密充填(HCP)もまた密接に関係した充填である．
この充填の密度は，面心立方格子と同じである．
面心立方格子の最密充填におけるように，六方最密充填では各球が他の12個の球で囲まれている．この充填のために最小ベクトルのドロネー(Delaunay)メッシュを取ることは，外側の12個の球の中心を繋ぎ，その辺が，囲んでいる多面体の面となるようにすることと同じである．
これは，結果として，同相双三角台塔として知られる多面体になる．
