リーマン(Riemann)予想を調べる
ベルンハルト・リーマン(Bernhard Riemann)による1859年の画期的な論文で初めて発表されたリーマン予想は，奥深い数学予想であり，非自明なリーマンゼータ関数の零点，つまり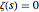 
であるような
, 
, 
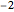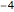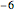, …以外のリーマンゼータ関数
の値はすべて「臨界線」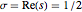 
上にあるというものである．ここで
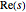は複素変数 
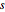の実部を表す．
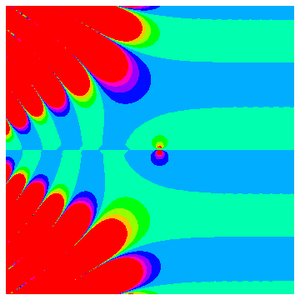
リーマンゼータ関数は負の実軸に沿って無限に振動する一方，これは正の実軸に沿って漸近的に1に近付く．
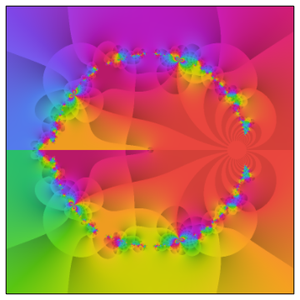
この挙動は，臨界線に沿ってより複雑になる．
実際，先のプロットは複素平面で発生する真の複雑性をよりよく表している．
リーマンゼータ関数の最初の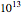
個の非自明な零点は検定され，リーマン予想を満足することが分かっている．それゆえこのような十分な数値的証拠がある上，かなりの努力がなされているにもかかわらず，この250年の間，誰もこの予想を証明することができていないのは驚きである．
数学の結果の多くは「リーマン予想が真であるとする」としている．つまり，リーマン予想が証明されることによって，その他の多数の結果も直ちに確定されるということである．リーマン予想の代替の定式化も数多く存在する．RiemannHypothesisFormulation実体領域は，これらを収集しようと試みている．
現在このコレクションには，合計でおおよそ70の定式化が含まれている．
これらの式はその半分の族にグループ分けすることができる．
もともとのリーマン予想の形式は，次の簡単な形式で限定記号を使った演算として表すことができる．
これは原理上は計算可能であるが，誰もリーマン予想を構築する方法を知らないため，それに限定記号消去を適用すると評価できなくなってしまう（もしMathematicaがこの場合の限定記号を解くことができれば，リーマン予想の妥当性を証明することができるだろう）．
RiemannHypothesisFormulation領域に存在する別の式のタイプを調べる．
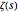に深く関係する関数である 
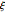関数の導関数によって与えられる式の正値性に関するリーマン予想の最も有名な代替の文は，おそらくLiの不等式である．Liの不等式として知られるこの式は次のように正式に述べることができる．
Wolfram言語は不等式内部の式についての閉形式を直接計算することができる（大規模な指標で計算すると，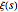
の導関数によって満足される既知の再帰関係の使用が必要になる）．まず式から不等式を抽出する．
Liの定数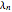 
を定義する．すべての正の 
に対するこの定数の正値性はリーマン予想に等しい．
厳密に計算し，定数を5次まで数値化すると，それらが実際に正であることが証明される．
もちろんLiの不等式は1つの代替式に過ぎない．多数の数学者がリーマン予想に対して複数の定式を導いてきた．次は，コレクション中の異なる定式数によって順序を付けた定式者のリストである．
これで，美しいが頑固に解けないリーマン予想につぎ込まれた高レベルの活動をある程度まで示す，数学者のタイムラインを構築することができる．
