連分数の恒等式を可視化する
"ContinuedFraction"実体タイプには多数の事前計算された関連する特性とともに，何千もの連分数の恒等式が含まれている．
例えば，余弦関数に対する既知の連分数恒等式からなる実体クラスを取り出すことが簡単にできる．
余弦に対する実体の明示的なリストを得るためには，EntityListを適用する．
恒等式を明示的に見ることができる．
左辺が明示的にCos[z]（引数に追加のスケール因子がない）である恒等式を選ぶ．
次数2から12までの有限の偶数の近似分数を計算し，後続の近似分数が，次第に余弦関数のよりよい近似となる様子を可視化する．
ここで多数のより複雑な（しかし美しい）連分数恒等式を調べる．このうちの多くはラマヌジャン(Ramanujan)に関連する．
これらの恒等式には，ヤコビ(Jacobi)のテータ関数およびポッホハマー(Pochhammer)記号として知られる数学関数が関わっている．
これらのうちの最後のロジャース=ラマヌジャン(Rogers-Ramanujan)連分数は変数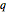 
のベキ乗をネストすることよって定義された特に美しい連分数の恒等式である．
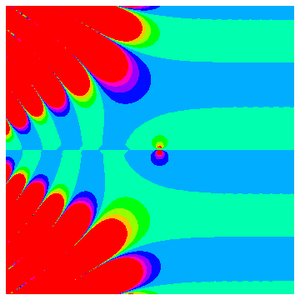
この定義は簡単であるが，ロジャース=ラマヌジャン連分数は複素平面上で非常に豊かな構造を持つ．これを見るために，実部，虚部，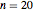 
の法を等高線プロットとしてプロットすることによって，
番目の近似分数の複雑な構造を表示する．
完全なWolfram言語入力を表示する
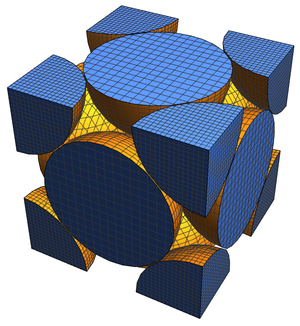
3Dプロットにすると，少し異なって見える．
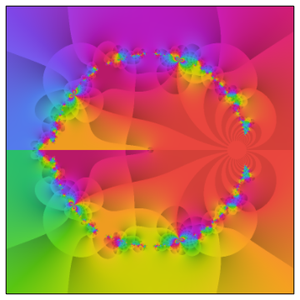
ロジャース=ラマヌジャン関数の視覚的探究を終えるために，ComplexPlotを使って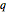 
が複素平面上で変化するときの
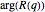の複素引数をプロットし，その複雑な構造のいくつかについて詳しい視覚表現を得る．
