群関係と生成元を調べる
"FiniteGroup"実体領域は，有限位数の有名な群に関する詳細データを保持している．
群のリストには23の散在群が含まれており，その中で最も大きいのはモンスター群である．そのうちの最初のいくつかを群の位数とともにここで表にした．
有限群から多数のおもしろい可視化が作成できる．簡単なものにArrayPlotを使った乗算表のプロットがあるが，これはもとになっている帯とブロックの構造を表している．
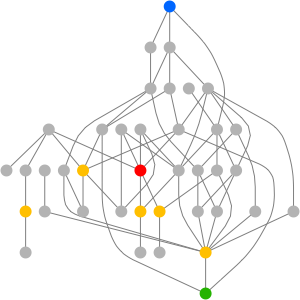
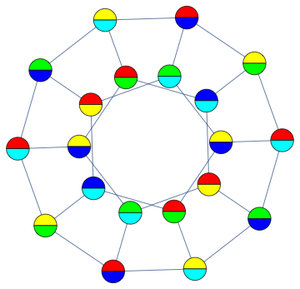
群を可視化する別の方法としてケイリー(Cayley)グラフがある．与えられたグラフと生成系に関連付けられたケイリーグラフは，それぞれの群の元に関連付けられた1つの頂点，および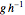
が生成系のメンバーであるときは常に，有向辺
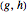を持つ有向グラフとして定義される（ケイリーグラフは生成系の選択に依存することもある）．
例えば，アーベル群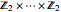 
のケイリーグラフは，双向超立方体グラフ 
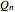で与えられる．
超立方体グラフとの対応は，対応する超立方体"Graph" 実体を返すToEntityを使って確認することができる．
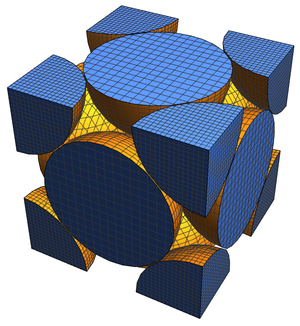
四面体結晶点群のケイリーグラフは，準正多面体（アルキメデスの立体）のスケルトンから導かれた名前付きのグラフに対応する．
ここでも，連想グラフをプログラムで取得することができる．
今度はこれらの連想グラフを，これらのグラフに対応するスケルトンを有する"Polyhedron"実体領域の実体に変換できる．
