Explore Torus Knots
The "Knot" entity domain contains an exhaustive enumeration of knots with small numbers of crossings.
The knots on fewer than six crossings are mostly named and can be extracted using an implicitly defined entity class.
They can be directly visualized using the "Image" property.
Similar visualizations are available for more complicated knots.
A multitude of properties is also available for all knots.
In addition to the standard tabulated knots up to 10 crossings, the "Knot" domain also contains additional entities corresponding to some parametrized families of knots, the most notable being torus knots.
A 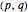 torus knot can be visualized as the knot obtained by looping a string through the hole of a torus
torus knot can be visualized as the knot obtained by looping a string through the hole of a torus 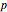 times with
times with 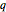 revolutions before joining its ends, when
revolutions before joining its ends, when  and
and 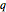 are relatively prime positive integers.
are relatively prime positive integers.
It is relatively straightforward to visualize a torus knot on the surface of a base torus using the "Torus" entity from the "Surface" entity domain.
An attractive visualization of a high-order torus knot can be obtained by randomly coloring the line segments in its knot diagram.
Similarly, picking torus knots at random and coloring the segments of their knot diagrams by hue gives rainbow-colored torus knots that resemble spirogram patterns.
Rainbow coloring in three dimensions gives another attractive visualization.