グラフの分数彩色
Webページのランキング,電子回路の設計,ソーシャルネットワークの分析,流通管理等の幅広い分野をカバーする現代の問題の多くは,グラフ理論のツールを使って立式し解決することができる.グラフの構築や操作とグラフを使った計算のための多くの関数に加え,Wolfram言語には多数のグラフが含まれている.
"Graph"実体領域は,興味深い無向グラフを,できるだけ多くの既知のあるいは計算可能な特性とともに分類することを目標としている."Graph"実体は,6000以上の単純グラフと500以上の事前計算された特性を提供しており,この数は今も増え続けている.
"Graph"実体のフレームワークには,ほとんどのグラフの事前計算された「素敵な」埋込みも含まれている.
"Graph"特性が返すオブジェクトは単なるグラフではなく,Wolfram言語の実際のGraphオブジェクトである点に注意のこと.
各グラフ実体には,そのグラフが属す数学クラスの詳細なリストが含まれている.
また,グラフ実体とトップレベルのグラフオブジェクトを繋ぐ2つの関数もある.ToEntityは,未知の単純グラフを実体(存在すれば)に変換する.
その逆はFromEntityによって与えられるが,これは"Graph"特性を使うことに等しい.
"Graph"実体領域で利用可能なデータの広がりを知るために,いわゆるグラフの分数彩色数を考えてみよう.分数彩色数は,通常の彩色数を彩色について一般化したものである.ここで,頂点はそれぞれが指定された重み割合を持ち,隣接する頂点が同じ色にならないようにそれぞれ複数の色で彩色される.
例えば,12面体グラフの彩色数は3色(隣接する2頂点が同じ色にならないように塗り分けるためには最低3色必要)であるが,分数彩色を使うと,5/2という分数の彩色数が与えられる(後で説明するインスタンス化の1つで,5色が重み1/2で各ノードに割り当てられる).
グラフ実体領域は,多くのグラフについて通常の彩色数と分数彩色数の両方を,これらの最小値を達成する具体的な彩色とともに含んでいる.例えば,12面体グラフの彩色数は3である.
この値を実現する彩色は以下のようにして取り出すことができる.
この埋込みと彩色データを組込みのグラフ機能と一緒に使って可視化を作成するのは非常に簡単である.
上記の図を見れば(あるいはプログラムを使えば)確認できるように,同じ色の隣接頂点は存在しない.
分数彩色はもう少し複雑だが,基本的に,頂点が異なる色を分数割合で含むことを許すことで,各頂点が一意的な色を持つという制約条件が緩和される.分数彩色数はすべての頂点について分数割合を合計することで定義され,しばしば「より少ない」色数(必ずしも整数ではないが)での彩色が可能になる.例えば,12面体グラフの分数彩色数は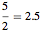 で,通常の彩色数の3よりも少ない.
で,通常の彩色数の3よりも少ない.
分数彩色を得るためには,"MinimumWeightFractionalColoring"特性を使って頂点と異なる色の重みのリストを得る.
例えば,上述の出力は,最小分数彩色は5色を使うと可能で,最初の色が頂点3, 5, 9, 12, 13, 15, 16, 20に重み1/2で,という具合になることを意味している.各色が1/2という同じ重みで適用されるので,全体的な分数彩色数は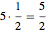 になる.
になる.
この場合は各色の割合が1/2に等しいので,可視化は簡単に求まる.まず,各頂点の二色を求める.
例として,上述のリストは最初の頂点が色4と色5を,2番目の頂点もまた色4と色5を使い,3番目の頂点は色1と色5を使う,という具合になる.次に数値による色指標を実際の色に変換する.
可視化の最終段階は,適切に彩色された2つの半円からなる頂点形状を定義することである.
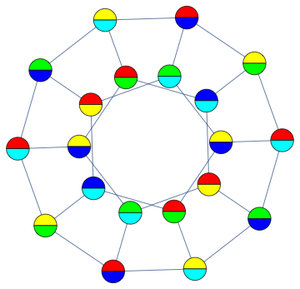
すべてのが揃ったら,12面体グラフの最小分数彩色が表示できる.
期待されるように,この分数彩色では同じ色の隣接頂点はない.
分数彩色数は一意的に分布してはいないが,特定の値に集まる傾向がある."Graph"実体領域の全グラフについての事前計算されたデータのヒストグラムを作ると,他にも集中している値はあるが,値が整数の周りに集まっていることが分かる.
BubbleChartを使うと,各分数彩色数を持つグラフの数を(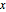 軸に分子,
軸に分子,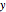 軸に分母を使って)プロットして,分布をより詳細に調べることができる.
軸に分母を使って)プロットして,分布をより詳細に調べることができる.