Visualize Continued Fraction Identities
The "ContinuedFraction" entity type contains thousands of continued fraction identities together with many precomputed associated properties.
For example, it is easy to retrieve an entity class consisting of known continued fraction identities for the cosine function.
To obtain an explicit list of entities for cosine, apply EntityList.
You can also view the identities explicitly.
Now pick out identities where the left-hand side is explicitly Cos[z] (with no additional scale factor in the argument).
Compute the finite even convergents of orders 2 to 12 and visualize how subsequent convergents become increasingly better approximations to the cosine function.
Now explore a number of more complicated (and beautiful) continued fraction identities. A number of these are associated with Ramanujan.
These identities involve the mathematical functions known as Jacobi theta functions and Pochhammer symbols.
The last of these (the Rogers–Ramanujan continued fraction) is a particularly beautiful identity defined by nesting powers of a variable  .
.
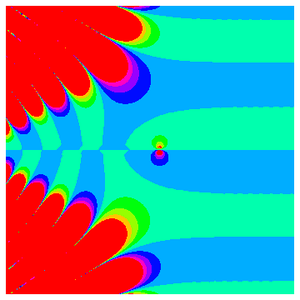
While its definition is simple, the Rogers–Ramanujan continued fraction has a very rich structure in the complex plane. To see this, show the complex structure of the  th convergents by plotting the real part, imaginary part and modulus for
th convergents by plotting the real part, imaginary part and modulus for 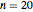 as contour plots.
as contour plots.
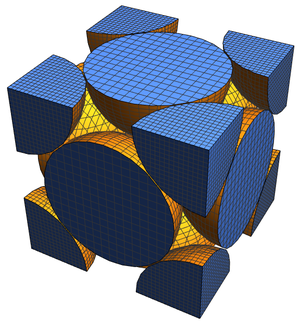
A slightly different view can be obtained by making 3D plots.
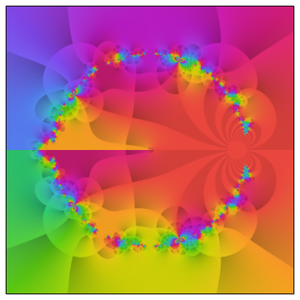
To conclude the visual exploration of the Rogers–Ramanujan function, use ComplexPlot to obtain a detailed view of some of its intricate structures by plotting the complex argument of  as
as 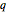 varies in the complex plane.
varies in the complex plane.