Wolfram 语言™

可视化连续分式恒等式

"ContinuedFraction" 实体类型含有上千个连续分式恒等式，以及预先计算好的相关属性。

例如，很容易获取由已知的余弦函数的连续分式恒等式组成的实体类别。

应用 EntityList 获取余弦函数的实体列表。

还可以明确显示恒等式。

现在选出左侧为 Cos[z]（参数中没有其他缩放因子）的恒等式。

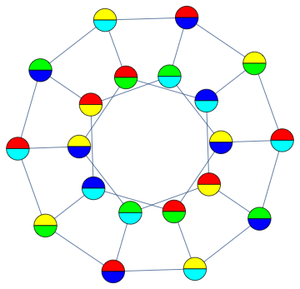
计算 2 到 12 的偶数阶数的有限收敛，并可视化阶数增大时更好地近似余弦函数的情况。

现在研究几个更复杂（美妙）的连续分式恒等式。有几个与 Ramanujan 有关。

这些恒等式涉及 Jacobi theta 函数和 Pochhammer 符号。

最后一个式子（Rogers–Ramanujan 连续分式）尤为美妙，是一个由变量 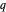的嵌套幂定义的恒等式。

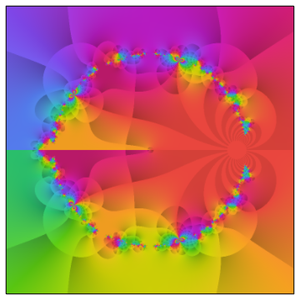
虽然它的定义很简单，但 Rogers–Ramanujan 连续分式在复平面上具有非常丰富的结构。要看到这一点，我们来绘制 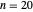时实部、虚部和模的等高线图，以查看 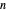阶收敛的复杂结构。

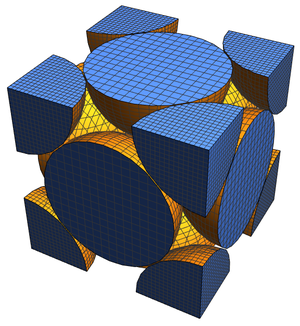
通过制作 3D 图可获取略微不同的视图。

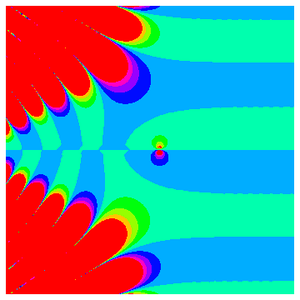
最后，用 ComplexPlot 获取 Rogers–Ramanujan 函数复杂结构的详细视图，绘制 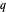在复平面上变化时 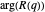的辐角。