Visualize identidades de frações contínuas
O tipo de entidade "ContinuedFraction" contém milhares de identidades de fração continuada, juntamente com muitas propriedades associadas pré-calculadas.
Por exemplo, é fácil extrair uma classe de entidade que consiste em identidades de fração contínua conhecidas para a função cosseno.
Para obter uma lista explícita de entidades para cosseno, aplique EntityList.
Você também pode ver as identidades explicitamente.
Agora escolha identidades onde o lado esquerdo é explicitamente Cos[z] (sem nenhum fator de escala adicional no argumento).
Calcule os convergentes finitos e pares das ordens 2 a 12 e visualize como os convergentes subsequentes se tornam aproximações cada vez melhores da função cosseno.
Agora, explore várias identidades de fração contínua mais complicadas (e bonitas). Várias delas estão associados ao Ramanujan.
Essas identidades incluem as funções matemáticas conhecidas como funções teta de Jacobi e símbolos de Pochhammer.
A última delas (a fração continuada de Rogers–Ramanujan) é uma identidade particularmente bonita definida pelo potencial de aninhamento de uma variável 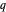 .
.
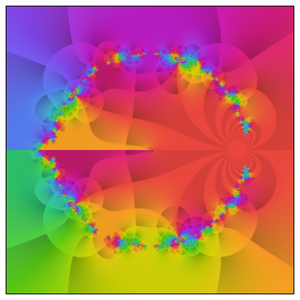
Embora sua definição seja simples, a fração continuada de Rogers–Ramanujan possui uma estrutura muito rica no plano complexo. Para ver isso, mostre a estrutura complexa dos 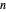 th convergentes traçando a parte real, a parte imaginária e o módulo para
th convergentes traçando a parte real, a parte imaginária e o módulo para 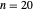 como gráficos de contorno.
como gráficos de contorno.
Uma visão ligeiramente diferente pode ser obtida através de gráficos 3D.
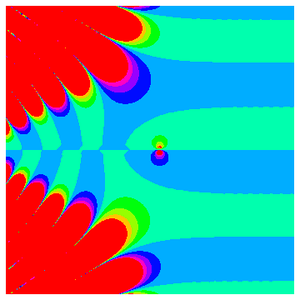
Para concluir a exploração visual da função Rogers–Ramanujan, use ComplexPlot para obter uma visão detalhada de algumas de suas estruturas complexas, fazendo um gráfico do argumento complexo de 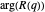 conforme
conforme 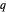 varia no plano complexo.
varia no plano complexo.