Identitäten von Kettenbrüchen visualisieren
Die Entität "ContinuedFraction" umfasst Tausende Kettenbruch-Identitäten sowie viele vorberechnete verbundene Eigenschaften.
So ist es beispielsweise einfach, eine Entitätsklasse abzurufen, die aus bekannten Kettenbruchidentitäten für die Cosinusfunktion besteht.
Mit EntityList erhalten Sie eine explizite Liste von Cosinus-Entitäten.
Sie können die Identitäten auch explizit anzeigen.
Wählen Sie nun Identitäten aus, bei denen die linke Seite explizit Cos[z] ist (ohne zusätzlichen Skalierungsfaktor im Argument).
Berechnen Sie die geraden finiten Konvergenzen der Ordnungen 2 bis 12 und visualisieren Sie, wie nachfolgende Konvergenzen zu immer besseren Annäherungen an die Cosinusfunktion werden.
Erkunden Sie nun eine Reihe von komplizierteren (und schöneren) fortlaufenden Bruchidentitäten. Eine Reihe davon ist mit Ramanujan verbunden.
Diese Identitäten beinhalten die mathematischen Funktionen, die als Jacobi-Theta-Funktionen und Pochhammer-Symbole bekannt sind.
Die letzte davon (der Rogers–Ramanujan-Kettenbruch) ist eine besonders schöne Identität, die durch Verschachtelungspotenziale einer Variablen 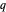 definiert ist.
definiert ist.
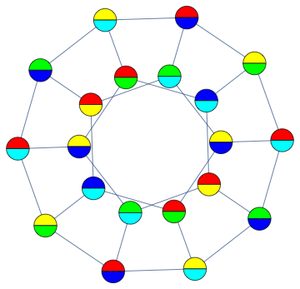
Trotz seiner einfachen Definition hat der Rogers–Ramanujan-Kettenbruch eine umfangreiche Struktur in der komplexen Ebene. Um dies zu veranschaulichen, zeigen Sie die komplexe Struktur der 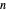
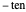 Konvergenten, indem Sie Realteil, Imaginärteil und Modul für
Konvergenten, indem Sie Realteil, Imaginärteil und Modul für 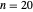 als Konturdiagramme plotten.
als Konturdiagramme plotten.
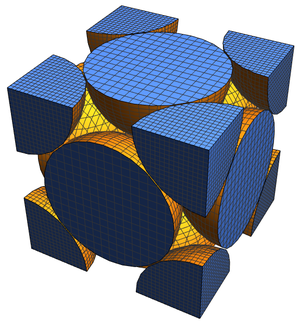
Eine etwas andere Ansicht kann durch die Erstellung von 3D-Plots erzeugt werden.
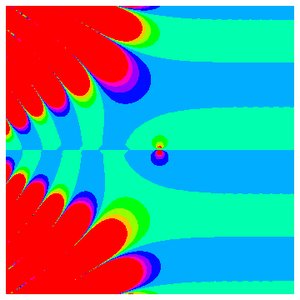
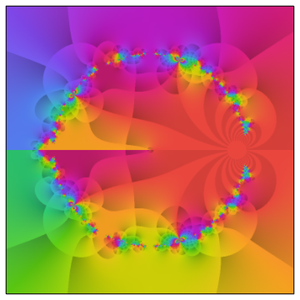
Zum Abschluss der visuellen Auseinandersetzung mit der Rogers–Ramanujan-Funktion können Sie mit ComplexPlot eine detaillierte Ansicht einiger seiner komplizierten Strukturen erzeugen, indem Sie das komplexe Argument von 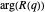 plotten, da
plotten, da 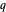 in der komplexen Ebene variiert.
in der komplexen Ebene variiert.