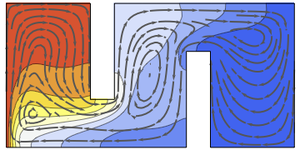
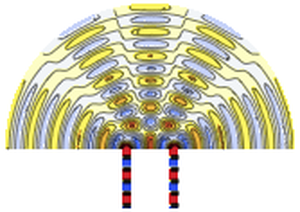
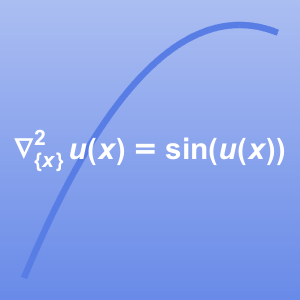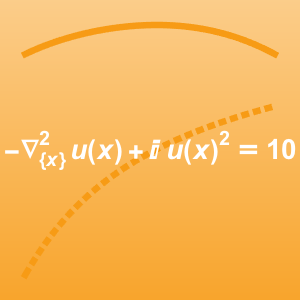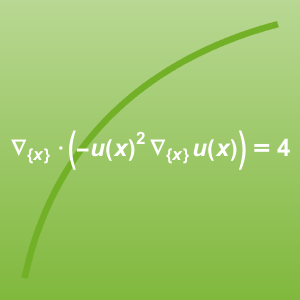Energietransport
Lösen Sie ein multiphysikalisches Problem, das die Navier–Stokes-Gleichung mit einer Wärmegleichung koppelt:
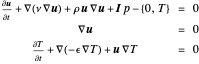
Hier ist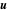 
das vektorielle Geschwindigkeitsfeld, 
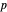der Druck und 
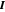die Identitätsmatrix. 
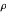und 
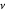sind Dichte bzw. dynamische Viskosität. 
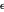ist die Wärmekapazität der Flüssigkeit und 
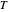die Temperatur.
Geben Sie die Parameter und eine rechteckige Fläche mit Löchern an.
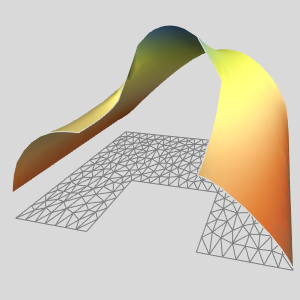
Visualisieren Sie die Region.
Geben Sie eine Prandtl-Zahl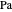 
und eine Rayleigh-Zahl 
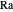an.
Definieren Sie durch eine Boussinesq-Approximation eine viskose Navier–Stokes-Gleichung, die an eine Wärmeleitungsgleichung gekoppelt ist. Verwenden Sie die festgelegten Materialparameter.
Legen Sie Haftbedingungen für die Geschwindigkeiten an allen Wänden fest.
Legen Sie einen Bezugsdruckpunkt fest.
Geben Sie eine Temperaturdifferenz zwischen der linken und rechten Wand an.
Ersetzen Sie Parameter in den Randbedingungen.
Legen Sie die Anfangsbedingungen so fest, dass das System in Ruhelage ist.
Beobachten Sie den Fortschritt der Zeitintegration und die Gesamtzeit, die benötigt wird, um die PDE mit einem Gitter mit bestimmtem Abstand zu lösen, indem Sie die Geschwindigkeiten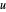 
und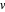 
und die Temperatur 
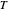mit zweiter Ordnung und den Druck 
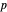mit erster Ordnung interpolieren.
Erstellen Sie eine Visualisierung des Rands der Region.
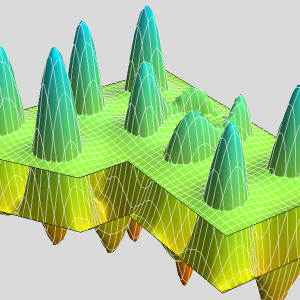
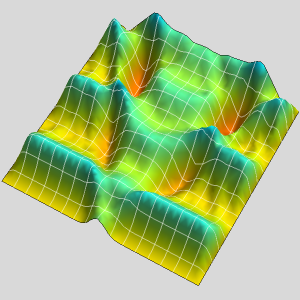
Visualisieren Sie die Druckverteilung.
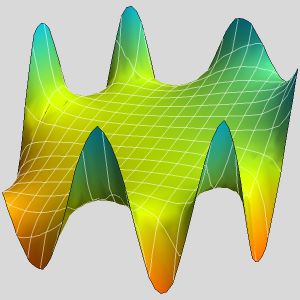
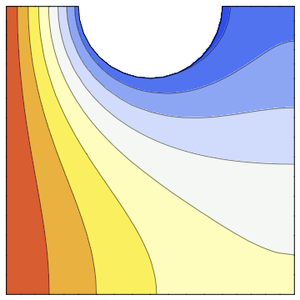
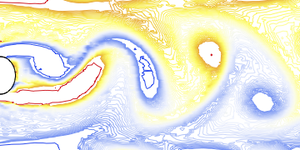
Visualisieren Sie die Temperaturverteilung.
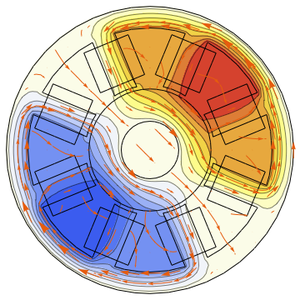
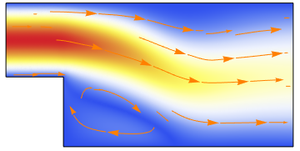
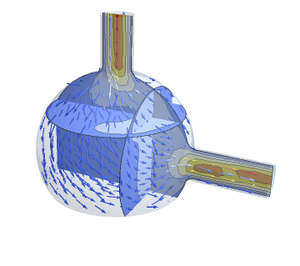
Visualisieren Sie das Geschwindigkeitsfeld.
Animieren Sie die Änderungen der Temperatur- und der Geschwindigkeitströmungslinien.
Es mag auch interessant sein, das andere Geschwindigkeitsfeld zu untersuchen, welches ensteht, wenn die Positionen der Cutouts vertauscht werden.
