Wolfram Language™

Modele as linhas de campo de uma distribuição de carga triangular

A Wolfram Language é uma linguagem computacional poderosa e eficiente para a comunicação científica entre as pessoas. Um ótimo exemplo disso está no domínio da entidade dos sistemas físicos. Para ter uma noção do escopo do que está disponível em "PhysicalSystem", veja uma amostra de entidades disponíveis:

Encontrar um determinado sistema físico de interesse é simplificado por sua categorização em classes de entidade. Atualmente, existem 27 classes de entidades não-disjuntas, das quais uma amostra é mostrada aqui.

Em vez de conter primariamente dados numéricos ou textuais, como no domínio "Country", o domínio do sistema físico contém principalmente fórmulas como as encontradas em livros didáticos. Para ver como eles podem ser usados, pegue o sistema de interesse para ser uma distribuição de carga triangular.

Uma maneira conveniente de ver o que está disponível para essa entidade é chamar "NonMissingProperties".

Em geral, entidades no domínio "PhysicalSystem" estão associados a um conjunto de "variáveis do sistema" que descrevem os parâmetros físicos gerais do sistema. Para a distribuição de carga triangular no espaço, essas são as cargas, 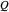, da distribuição e as coordenadas de seus vértices 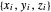para .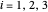

Qualquer propriedade pode depender dessas variáveis do sistema e, possivelmente, das coordenadas generalizadas do sistema. Por exemplo, olhando para a densidade de carga elétrica, você tem o seguinte:

Note, como é frequentemente o caso para as fórmulas retornadas por "PhysicalSystem", a cabeça desta expressão é Inactive[ReplaceRepeated]. Isso permite o uso de variáveis intermediárias, que podem tornar essas expressões menores e mais fáceis de compreender. Por exemplo, na fórmula apresentada anteriormente, 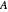é a área do triângulo e 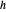representa a distância perpendicular do triângulo ao ponto de medição. As partes DiracDelta e Piecewise representam o fato de que a densidade de carga é diferente de zero apenas na distribuição triangular (infinitamente fina). Ao ativar a substituição, a expressão será reduzida para um, envolvendo apenas as variáveis do sistema e as coordenadas generalizadas.

Uma propriedade mais interessante de se ver pode ser o campo elétrico da distribuição de carga. Para visualização simplificada, considere as distribuições em duas dimensões (considerando 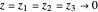). A forma do campo pode ser encontrada com o seguinte chamada EntityValue (o resultado é suprimido aqui por ser um pouco grande).

Escolhendo uma região triangular, colocando as coordenadas dos vértices em fieldForm e ativando, obtém-se uma solução direta e explícita, mas complexa, para o vetor de campo elétrico, como uma função de coordenadas no plano -.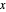

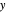A expressão anterior é bastante complicada, portanto, para facilitar a exibição, você pode apresentá-la em TraditionalForm Pane.

Finalmente, como último passo, tente visualizar as linhas de campo que fluem dessas fórmulas. Felizmente, a Wolfram Language tem a função integrada StreamDensityPlot para fazer exatamente isso. Você deve ter um pouco de cuidado para se livrar do QuantityVariables na expressão anterior, antes de fazer o gráfico, e as substituições que podem ser usadas para fazer isso são demonstradas a seguir. Adicionalmente, para fazer um gráfico mais interessante, sobreponha dois triângulos de carga e construa um Manipulate mostrando como seus campos interagem conforme sua posição relativa, o ângulo e as cargas são alterados. Veja o código e a animação resultante e aproveite para simular sistemas físicos na Wolfram Language!