유클리드의 원론
세계에서 가장 오래되고 지금까지 가장 영향력 있는 수학 논문의 하나로 고대 그리스 시대 알렉산드리아의 수학자 유클리드가 쓴 13권짜리 서적 "원론"을 꼽을 수 있습니다. "원론"에서 설명된 구조는 Wolfram 언어의 GeometricScene을 사용하여 표현하고 RandomInstance를 사용하여 시각화할 수 있습니다.
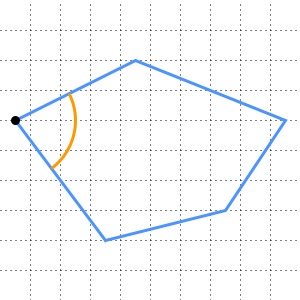
제1권의 명제 1은 임의의 두 점 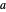 와
와  가 있을 때,
가 있을 때, 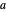 와
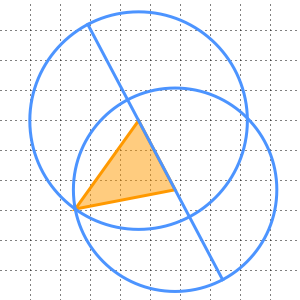
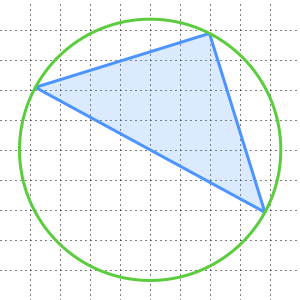
와 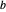 를 두 개의 정점으로 한 정삼각형을 만들 수 있다는 것입니다. 특히 반경이
를 두 개의 정점으로 한 정삼각형을 만들 수 있다는 것입니다. 특히 반경이 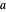 와
와 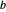 사이의 거리와 동일한
사이의 거리와 동일한 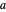 와
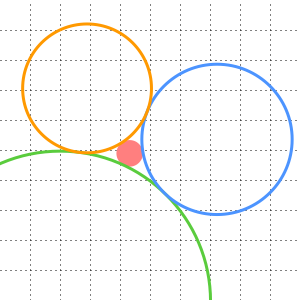
와 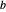 의 각각을 중심으로 하는 두 개의 원을 그립니다. 그러면 교점
의 각각을 중심으로 하는 두 개의 원을 그립니다. 그러면 교점 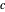 가 그 정삼각형의 세 번째 정점이 됩니다.
가 그 정삼각형의 세 번째 정점이 됩니다.
제1권의 명제 22는 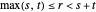 와 같은 임의의 양의 수량
와 같은 임의의 양의 수량 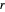 ,
, 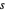 ,
, 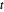 에 대해 변의 길이가
에 대해 변의 길이가 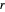 ,
, 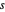 ,
, 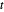 인 삼각형이 있다는 것에 의해 명제 1을 일반화하고 있습니다.
인 삼각형이 있다는 것에 의해 명제 1을 일반화하고 있습니다.
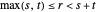 인 양의 수량
인 양의 수량 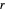 ,
, 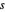 ,
, 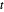 를 무작위로 선택합니다.
를 무작위로 선택합니다.
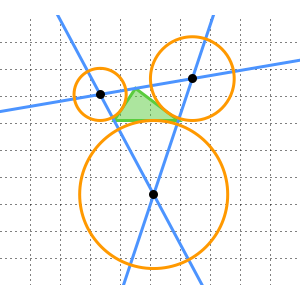
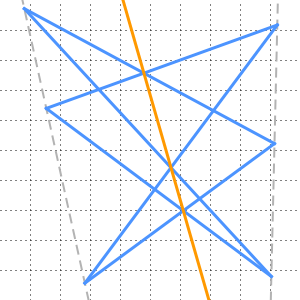
구조는 다음과 같이 진행됩니다. 점 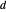 ,
, 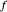 ,
, 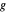 ,
, 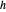 를 순서대로 통과하는 직선을 구축합니다. 여기서
를 순서대로 통과하는 직선을 구축합니다. 여기서 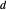 와
와 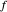 는
는 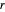 ,
, 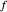 와
와 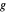 는
는 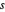 ,
, 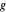 와
와 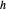 는
는 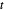 와 거리가 떨어져 있습니다.
와 거리가 떨어져 있습니다. 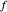 를 중심으로 하여
를 중심으로 하여 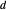 를 통과하는 원과
를 통과하는 원과 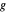 를 중심으로 하여
를 중심으로 하여 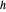 를 통과하는 원을 그립니다. 만약
를 통과하는 원을 그립니다. 만약 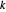 가 이들 원이 교차하는 점 중 하나라면,
가 이들 원이 교차하는 점 중 하나라면, 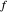 는
는 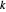 로부터
로부터 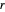 떨어져 있고,
떨어져 있고, 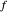 는
는 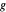 로부터
로부터 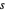 떨어져 있으며,
떨어져 있으며, 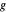 는
는 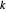 로부터
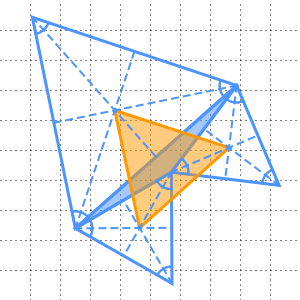
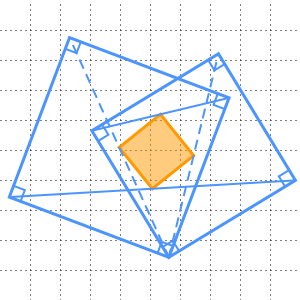
로부터 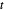 떨어져 있습니다. 따라서 점
떨어져 있습니다. 따라서 점 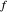 ,
, 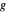 ,
, 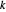 는 이러한 삼각형을 형성합니다.
는 이러한 삼각형을 형성합니다.