用 Pareto–Pickands 分布拟合幂尾型数据
Pareto–Pickands 分布,亦称为广义 Pareto 分布 (GPD),被引入来研究极端顺序统计量,并且通常用于描述超过某个高阈值的事件。Pareto–Pickands 分布常被用于保险、水文和气候学中。
Pareto–Pickands 分布也可以用来模拟幂尾型分布的超阈值 (exceedance),Wolfram 语言中有许多这样的分布,如 CauchyDistribution、DagumDistribution、LogGammaDistribution、ParetoDistribution、StudentTDistribution 等。
这种分布的高阶矩不存在。
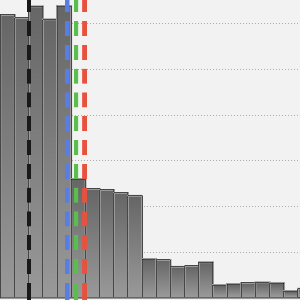
直方图显示样本有一个长尾。
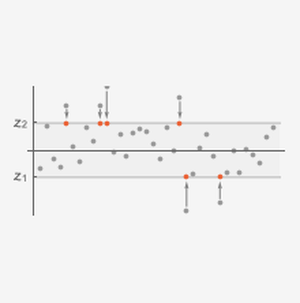
截断数据,保留尾部较大的数据。
将尾部数据拟合为 Pareto–Pickands 分布。
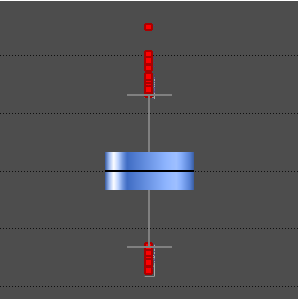
用分位数曲线检查拟合优度。
拟合优度检验。
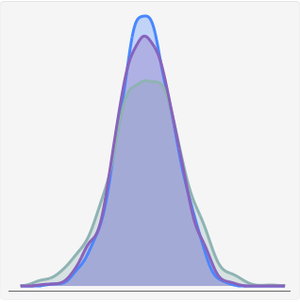
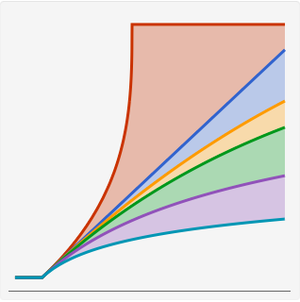
一个有趣的事实:标准的 Pareto–Pickands 分布是随机排序的;即对于 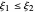 ,累积分布函数是有序的,对于所有的
,累积分布函数是有序的,对于所有的 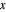 ,
,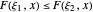 :
:
显示完整的 Wolfram 语言输入