Calibration of a Gauge
One of the fundamental steps in the handling of the uncertainty in measurements is its propagation through mathematical formulas to obtain the uncertainty of a derived magnitude.
Here example H.1 of the document Guide to the Expression of Uncertainty in Measurement is followed. That example describes the calibration of the length  of an end gauge by comparing it to a standard gauge of length
of an end gauge by comparing it to a standard gauge of length 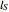 at
at ![]() . They have respective thermal expansion coefficients
. They have respective thermal expansion coefficients 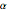 and
and 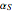 , and measurements are performed at temperatures
, and measurements are performed at temperatures 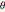 and
and 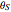 , both taken as differences with respect to the reference temperature of
, both taken as differences with respect to the reference temperature of ![]() .
.
This is then the difference in lengths.
Defining 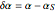 and
and 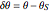 , we can then approximate
, we can then approximate  as follows, where all variables on the right hand side of this equation are now uncorrelated.
as follows, where all variables on the right hand side of this equation are now uncorrelated.
The calibration certificate for the standard end gauge gives this value at ![]() .
.
Thermal coefficient expansions are estimated as follows.
And these are the temperature differences.
Finally, this is the value given for the length difference 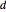 .
.
Therefore, the end gauge has this length at temperature ![]() .
.
A length of 50.000838 millimeters is obtained with an uncertainty of 32 nanometers, exactly reproducing the values in the preceding document.