Hypothèses pour les structures fines
La base de connaissances Wolfram Knowledgebase contient actuellement la meilleure valeur pour la constante de structure fine, ainsi que son incertitude. Cet exemple fournit une liste d'expressions numériques qui ont été proposées comme valeurs exactes possibles pour la constante de structure fine.
Exprimez les deux en utilisant Around.
Depuis plus d'un siècle, les scientifiques ont élaboré des hypothèses pour les formes fermées.
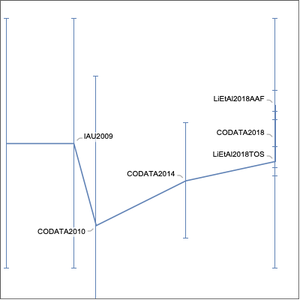
Formatez-les dans une grille de texte, en affichant le nom de l'auteur, l'année de la proposition et la forme proposée.
On peut mesurer la complexité d'une forme fermée, sous forme d'hypothèse entropique par le logarithme de la taille des entiers impliqués. Les fonctions mathématiques comptent de façon exponentielle.
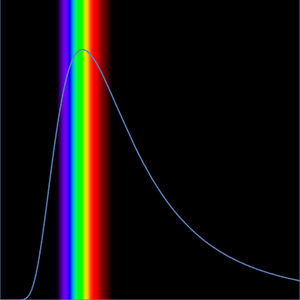
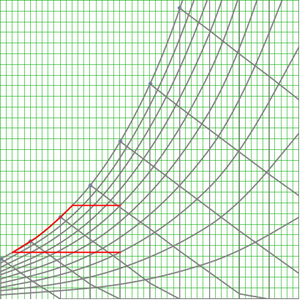
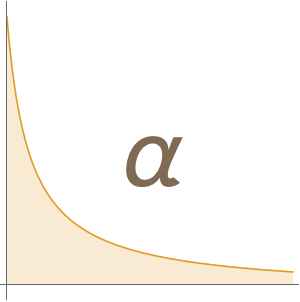
Les valeurs d'hypothèse qui sont plus proches de la valeur expérimentale sont typiquement plus complexes, et on ne connaît pas de forme fermée qui soit à la fois précise et courte. L'examen de la relation entre la complexité et les valeurs d'hypothèse, telles que représentées ici, suggère que les deux valeurs satisfont une inégalité de la forme 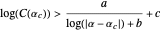 , où la courbe orange assume que
, où la courbe orange assume que 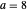 ,
,  , et
, et 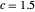 .
.