Mesures corrélées
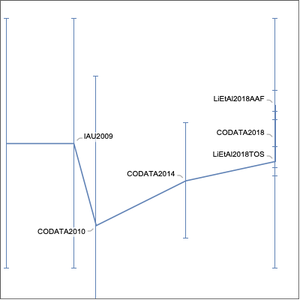
L'analyse des mesures produit souvent un ensemble de valeurs dont les incertitudes sont corrélées. Lorsqu'on utilise ces valeurs dans des calculs ultérieurs, il faut tenir compte de leurs corrélations.
Nous suivons ici l'exemple H.3 du document Guide to the Expression of Uncertainty in Measurement. Cet exemple illustre le processus d'étalonnage linéaire d'un thermomètre, en utilisant un ajustement par la méthode des moindres carrés.
Prenez un ensemble de paires 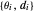 , où
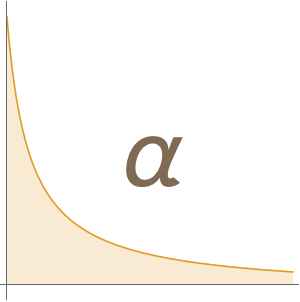
, où 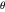 correspond à une différence de température en degrés Celsius par rapport à
correspond à une différence de température en degrés Celsius par rapport à ![]() , et
, et 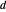 représente l'écart avec le résultat correct.
représente l'écart avec le résultat correct.
Calculez le meilleur ajustement linéaire.
Voici les paramètres de l'ajustement et leurs incertitudes estimées.
Voici les matrices de covariance et de corrélation de l'ajustement. Vous pouvez observer la corrélation non nulle entre les valeurs, exprimée dans l'élément non nul hors diagonale de la matrice de corrélation.
Elles sont liées comme suit.
Pour extrapoler la valeur de la différence de température en 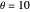 degrés Celsius, avec une estimation de l'incertitude, il serait incorrect d'effectuer l'un ou l'autre de ces deux calculs, basés sur des objets Around indépendants.
degrés Celsius, avec une estimation de l'incertitude, il serait incorrect d'effectuer l'un ou l'autre de ces deux calculs, basés sur des objets Around indépendants.
Ces deux calculs équivalents ignorent la corrélation entre les incertitudes des paramètres de l'ajustement. Pour les prendre en compte, les paramètres sont décrits à l'aide d'une expression VectorAround.