WolframOptimizationA Core Part of
Wolfram Language

Model, Solve & Analyze Designs.
Wolfram Optimization provides a comprehensive set of tools to find the best design or make the best decision given constraints, fully integrated with highly automated machine learning, statistics, immediately computable built-in data and more.
Optimization Modeling
Model objectives and constraints using mathematical functions, inequalities and inclusion. Define compact high-level models in a natural way with vector variables, vector inequalities and geometric regions. Create reusable models by programmatically constructing them from data, graphs and any other objects.
Linear & Convex Optimization
Solve large-scale convex optimization problems with global, fast and reliable methods. Convex optimization includes important classes such as linear, quadratic, second-order cone, semidefinite and conic optimization.
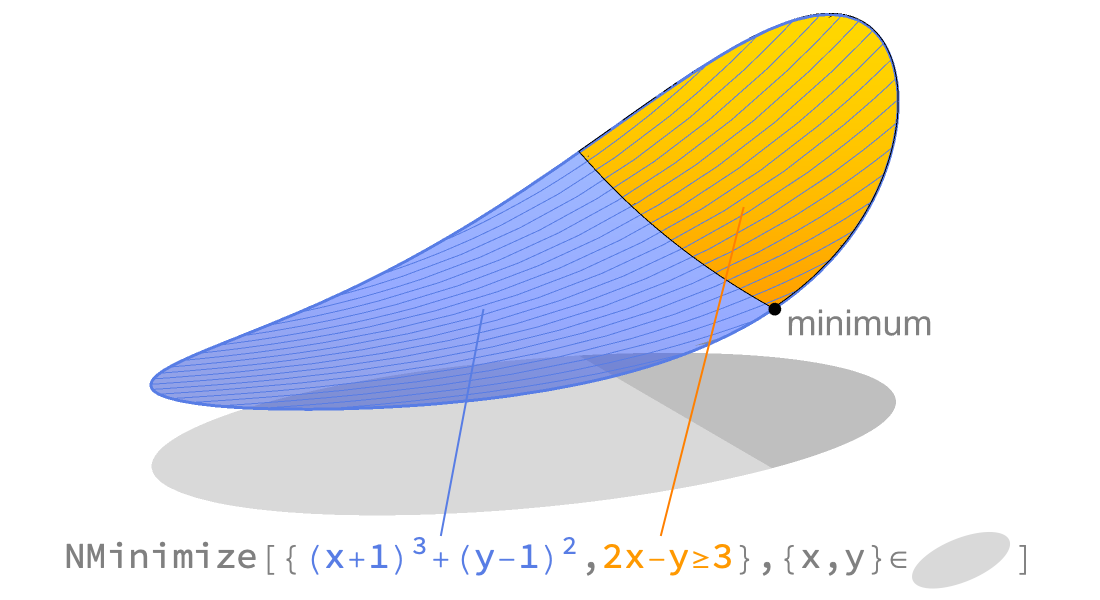
Local Optimization
Find a local optimum to unconstrained or constrained optimization problems. Local methods are fast and scalable and are often sufficient or used to build more elaborate methods. Solve using automated selection of methods ranging from quasi Newton to interior point, as well as computation of derivatives and compilation for efficiency.
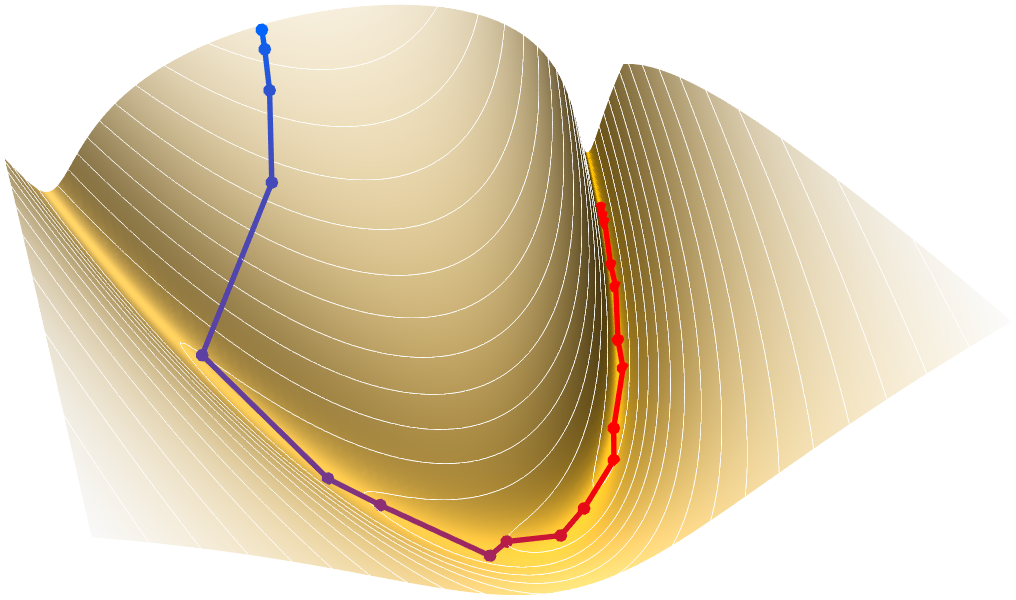
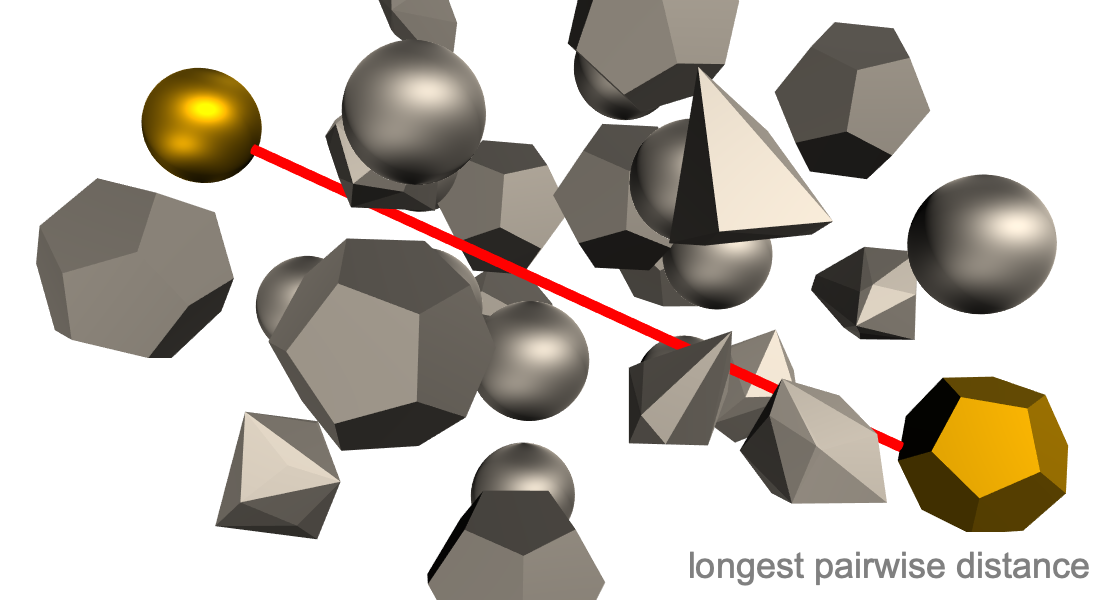
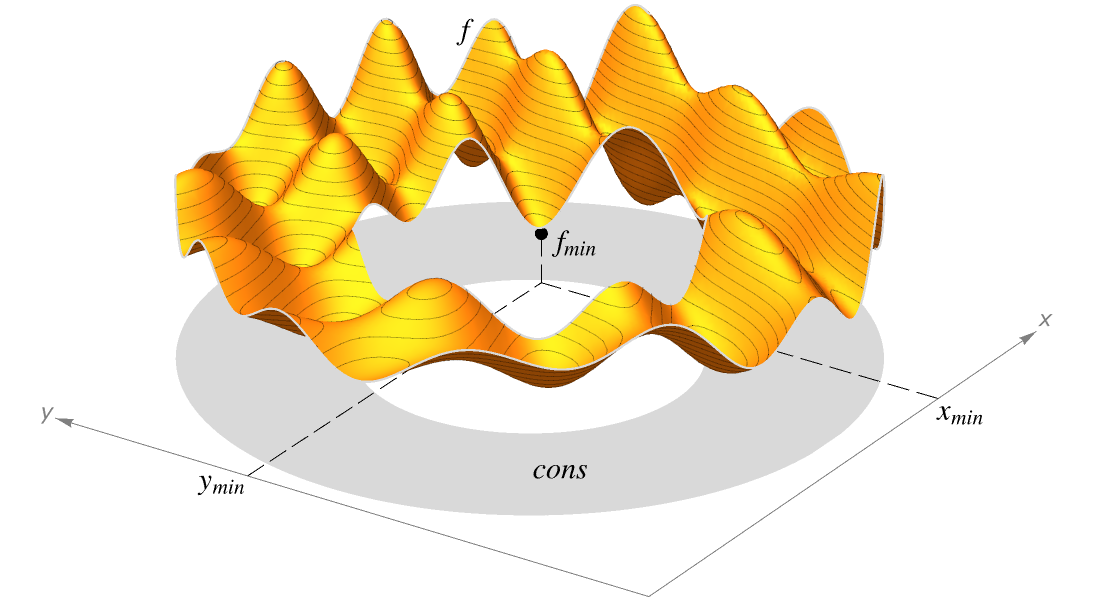
Global Optimization
Search for the best possible value for an objective within given constraints. The extra effort required for finding a global optimum is often valuable for financial, safety or efficiency reasons. Use a wide variety of methods from deterministic extensions to convex optimization to stochastic evolutionary methods.
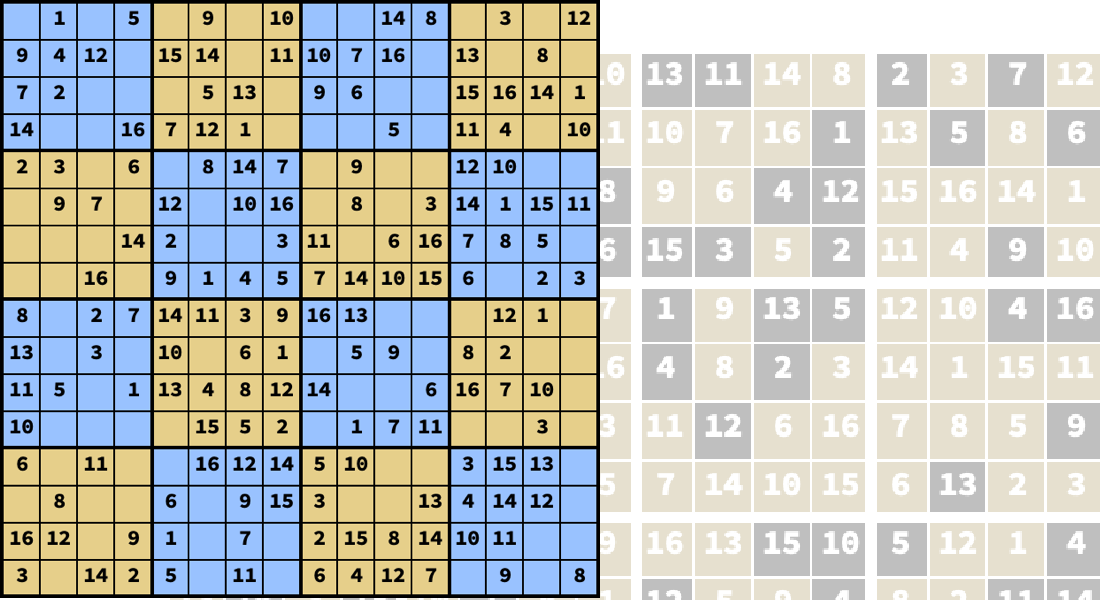
Mixed-Integer Optimization
Solve convex optimization problems where some of the decision variables can only have discrete or integer values. Discrete variables arise commonly in assignment, scheduling and routing problems. Use branch and bound, cutting plane and outer approximation methods to efficiently solve mixed-integer problems.
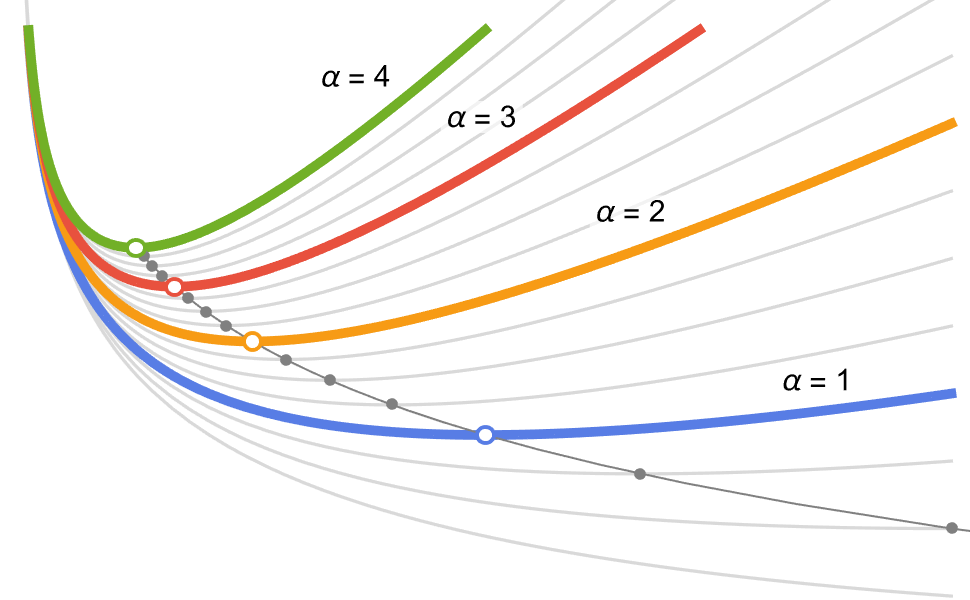
Parametric Optimization
Solve families of optimization problems by using parameters in objectives and constraints. Find many solutions efficiently (parameter sweeps), safe solutions for all values (robust optimization), expected solutions for random values (stochastic optimization) or sensitivity to changes in values (parametric sensitivity).
Symbolic Optimization
Get formulas for exact global solutions to optimization problems. Closed-form solutions are verified, reusable and combinable with other formulas. Use the same modeling language with exact symbolic or approximate numerical methods.

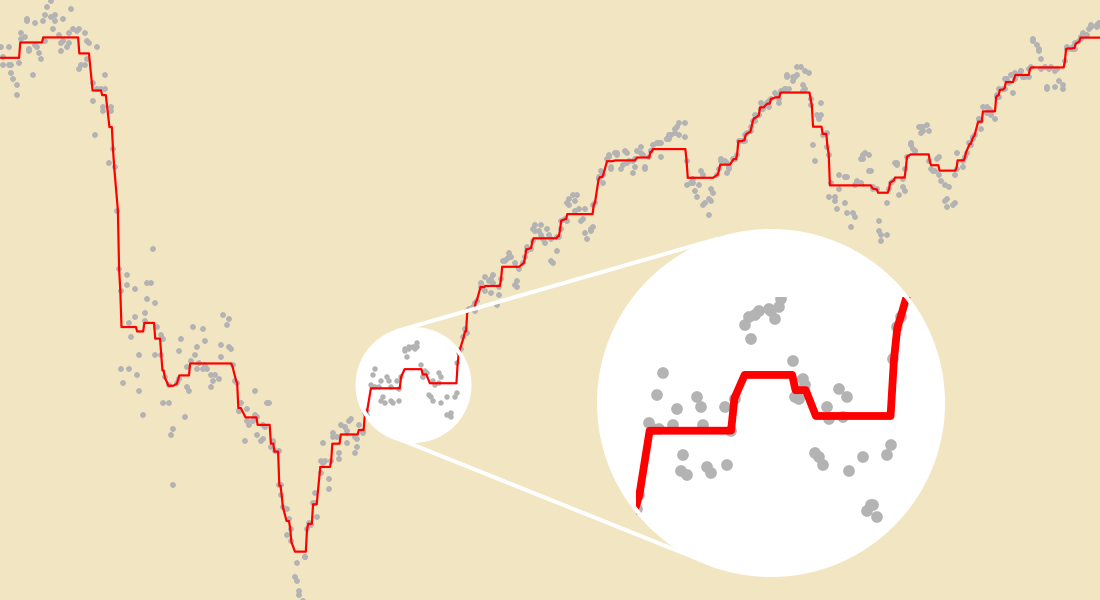
Optimal Fitting
Find model parameters that best fit a set of data points. Model fitting is the bridge between models and data, allowing easy inference of other values. Use linear and nonlinear fitting algorithms that use objectives including least squares, least absolute deviation, LASSO and ridge regression.
Special-Purpose Optimization
Easily model and efficiently solve important optimization tasks using dedicated functions. Use intuitive interfaces to solve neural network training, traveling salesman, knapsack and other special optimization problems.
Optimization Partners
Immediately leverage commercial solvers from Gurobi, MOSEK and FICO Xpress. For large-scale and mixed-integer optimization, best-in-class solvers can provide the needed edge. The optimization functions can automatically use methods for which you have a license.

Wolfram Optimization Documentation
Wolfram Optimization is an integrated part of Wolfram Language. The full system contains over 6,000 built-in functions covering all areas of computation—all carefully integrated so they work perfectly together.
Full Scope & Documentation