Numerisches Lösen von Polynomsystemen bei hoher Rechenleistung 

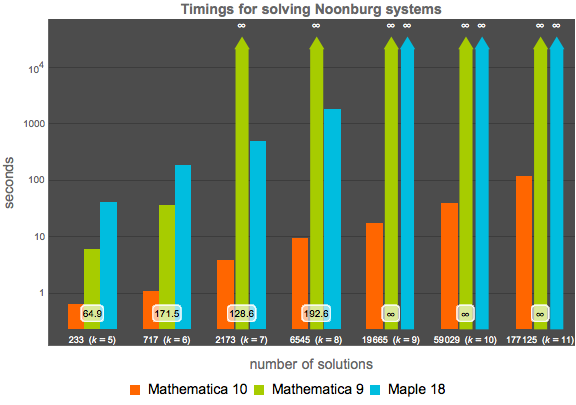
Mathematica 10 bietet einen neuen Homotopie-basierten numerischen Solver für Polynome. Diese Methode wird automatisch angewendet, wenn sie geeignet scheint. Die folgenden Diagramme vergleichen den Zeitbedarf dieses neuen Algorithmus mit der Gröbnerbasis-Methode von Mathematica 9 und den schnelleren der Maple 18-Befehlen solve oder Homotopy. Alle Tests wurden auf einem 16-CORE, 2.40 GHz 64-bit Linux-System mit aktiviertem Hyper-Threading bei einem Zeitlimit von 12 Stunden durchgeführt.

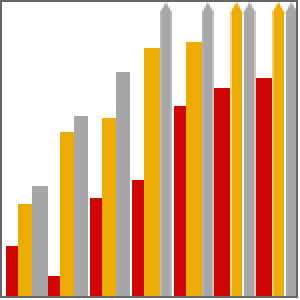
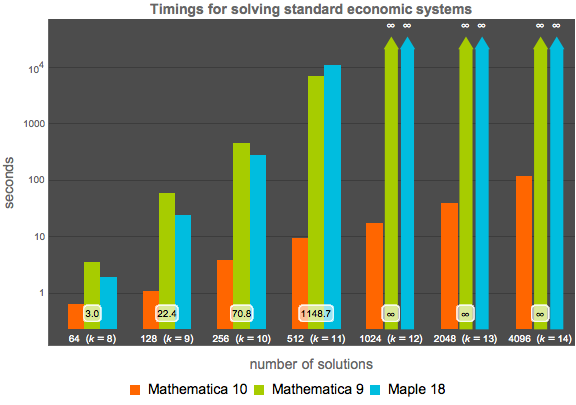
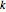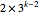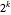Vergleich eines standardmäßigen Polynomsystem aus dem Bereich Wirtschaft in Variablen, Totalgrad und verschiedenen Lösungen, angegeben durch die folgende Formel:

In[1]:=

X eco[k_] := Append[ Table[(Subscript[x, i] + Sum[Subscript[x, j] Subscript[x, j + 1], {j, i, k - 2}]) Subscript[x, k] - i == 0, {i, 1, k - 1}], Sum[Subscript[x, i], {i, 1, k - 1}] + 1 == 0]

Für 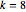zum Beispiel nimmt das System die folgende Form an:

In[2]:=

X Column[eco[8]] // TraditionalForm

Out[2]//TraditionalForm=

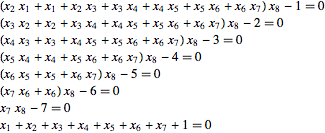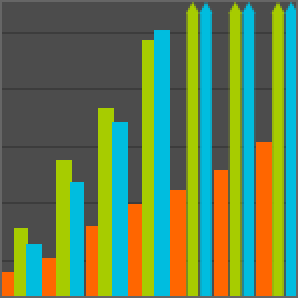
Vergleich für das standardmäßige neurale Noonburg-Netzwerksystem, angegeben durch die folgende Formel. Für 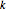Variablen hat dieses System den Totalgra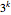d und 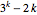unterschiedliche Lösungen.

In[3]:=

X noon[k_] := Table[Subscript[x, i] (Sum[Subscript[x, j]^2, {j, 1, k}] - Subscript[x, i]^2 - 1.1) + 1 == 0, {i, 1, k}]

Bei fünf Variablen zum Beispiel nimmt das System die folgende Form an:

In[4]:=

X Column[noon[5]] // TraditionalForm

Out[4]//TraditionalForm=

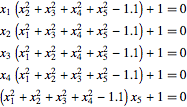Vergleich für das standardmäßige Katsura-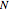-System der ferromagnetischen Gitter-Wahrscheinlichkeiten, das bei 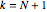Variablen den Totalgra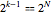d und 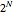verschiedene Lösungen hat. Das System N-ter Ordnung nimmt die folgende Form an:

In[5]:=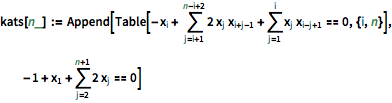

X kats[n_] := Append[Table[-Subscript[x, i] + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = i + 1\), \(n - i + 2\)]\(2\ \*SubscriptBox[\(x\), \(j\)]\ \*SubscriptBox[\(x\), \(i + j - 1\)]\)\) + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(i\)]\( \*SubscriptBox[\(x\), \(j\)]\ \*SubscriptBox[\(x\), \(i - j + 1\)]\)\) == 0, {i, n}], -1 + Subscript[x, 1] + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 2\), \(n + 1\)]\(2\ \*SubscriptBox[\(x\), \(j\)]\)\) == 0]

Bei 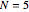zum Beispiel besteht das System aus sechs Gleichungen mit sechs Unbekannten.

In[6]:=

X Column[kats[5]] // TraditionalForm

Out[6]//TraditionalForm=
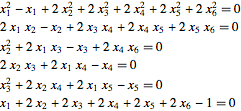