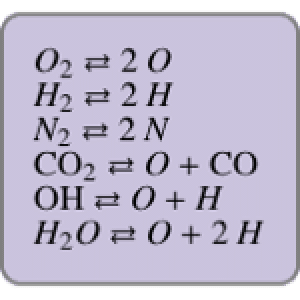Solução numérica de sistemas polinomiais de alto desempenho 

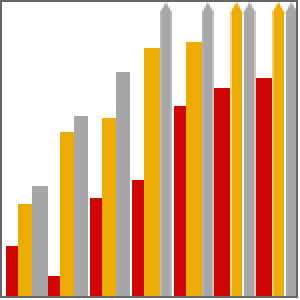
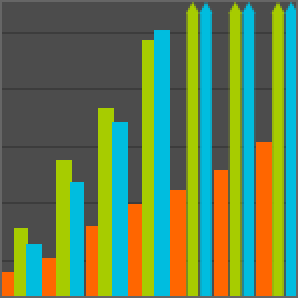
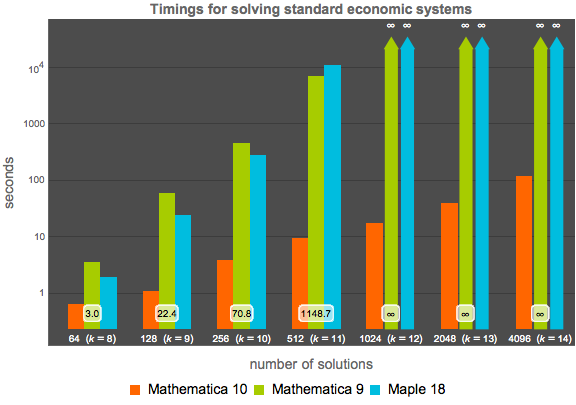
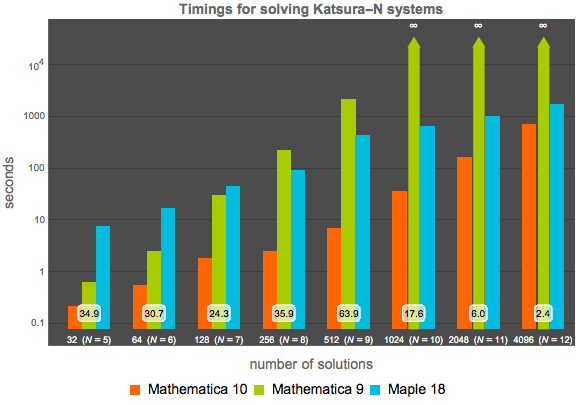
O Mathematica 10 inclui uma nova ferramenta de solução de polinômios numéricos baseada em homotopia. Esse método é automaticamente selecionado quando apropriado. Os gráficos a seguir comparam o tempo de espera desse novo algoritmo com o método de Base Gröbner do Mathematica 9 e com o mais rápido dos 18 comandos solve ou Homotopy do Maple 18. Todos os testes foram conduzidos em um sistema Linux de 64 bits, 2.40 GHz e 16 núcleos, com a tecnologia Hyper-Threading habilitada e um limite de tempo de 12 horas.

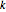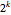Comparação de um sistema de economia padrão em variáveis, grau total , e soluções distintas , dado pela seguinte fórmula:

In[1]:=

X eco[k_] := Append[ Table[(Subscript[x, i] + Sum[Subscript[x, j] Subscript[x, j + 1], {j, i, k - 2}]) Subscript[x, k] - i == 0, {i, 1, k - 1}], Sum[Subscript[x, i], {i, 1, k - 1}] + 1 == 0]

Por exemplo, para 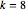, o sistema toma a seguinte forma.

In[2]:=

X Column[eco[8]] // TraditionalForm

Out[2]//TraditionalForm=

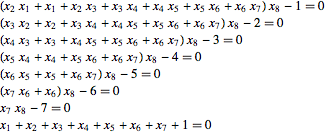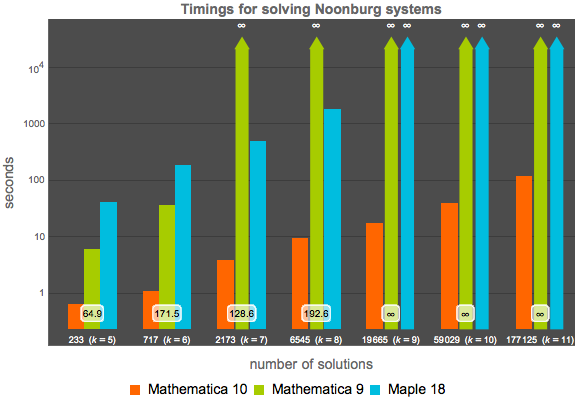
Comparação para o sistema de rede neural Noonburg padrão, dado pela seguinte fórmula. Para variáveis 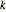, o sistema tem um grau total 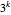e diferentes soluções.

In[3]:=

X noon[k_] := Table[Subscript[x, i] (Sum[Subscript[x, j]^2, {j, 1, k}] - Subscript[x, i]^2 - 1.1) + 1 == 0, {i, 1, k}]

Por exemplo, em cinco variáveis o sistema toma a seguinte forma.

In[4]:=

X Column[noon[5]] // TraditionalForm

Out[4]//TraditionalForm=

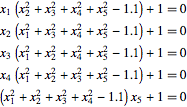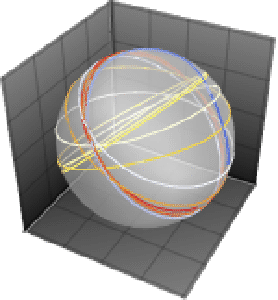
Comparação para o sistema Katsura-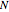 de probabilidades de retículos ferromagnéticos, o qual em 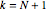variáveis tem grau total 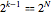e 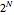soluções diferentes. O sistema de ordem- 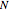toma a seguinte forma.

In[5]:=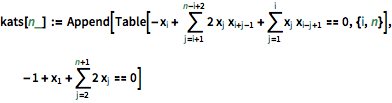

X kats[n_] := Append[Table[-Subscript[x, i] + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = i + 1\), \(n - i + 2\)]\(2\ \*SubscriptBox[\(x\), \(j\)]\ \*SubscriptBox[\(x\), \(i + j - 1\)]\)\) + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(i\)]\( \*SubscriptBox[\(x\), \(j\)]\ \*SubscriptBox[\(x\), \(i - j + 1\)]\)\) == 0, {i, n}], -1 + Subscript[x, 1] + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 2\), \(n + 1\)]\(2\ \*SubscriptBox[\(x\), \(j\)]\)\) == 0]

Por exemplo, para 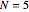o sistema tem seis equações em seis incógnitas.

In[6]:=

X Column[kats[5]] // TraditionalForm

Out[6]//TraditionalForm=
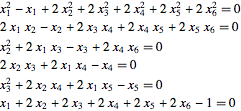