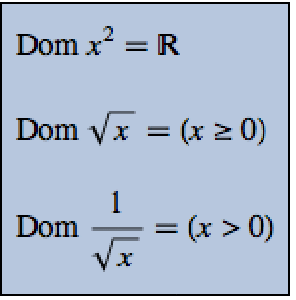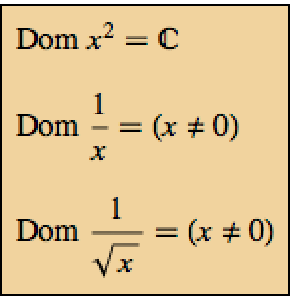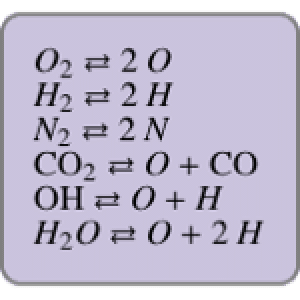多項式系の高性能数値解法 

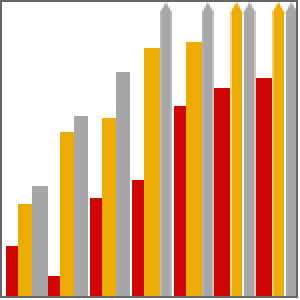
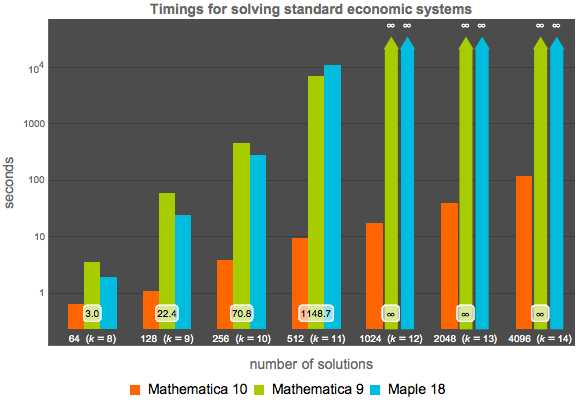
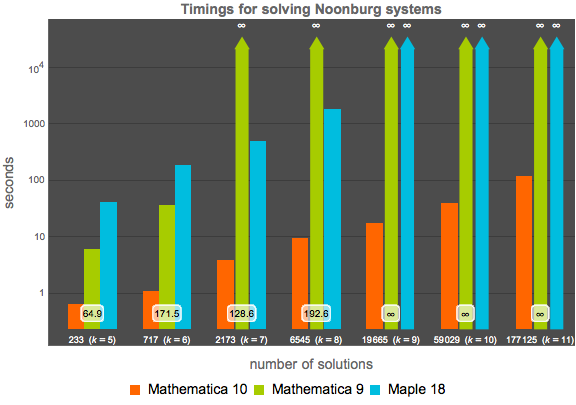
Mathematica 10には新しいホモトピーベースの多項式数値ソルバが含まれている．このメソッドは必要に応じて自動的に選ばれる．下の図は，この新しいアルゴリズムと Mathematica 9のグレブナー基底法およびMaple 18の solve あるいは Homotopy コマンドの速い方を比較したものである．すべてのテストは，ハイパースレッディングが有効な16コアの2.40 GHz 64ビットLinuxシステムで，時間制限を12時間として実行された．

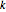個の変数，全次数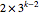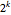， 個の異なる解における標準的なエコノミクス系の比較は以下の式で与えられる．

In[1]:=

X eco[k_] := Append[ Table[(Subscript[x, i] + Sum[Subscript[x, j] Subscript[x, j + 1], {j, i, k - 2}]) Subscript[x, k] - i == 0, {i, 1, k - 1}], Sum[Subscript[x, i], {i, 1, k - 1}] + 1 == 0]

例えば 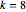の場合，系は以下の形式を取る．

In[2]:=

X Column[eco[8]] // TraditionalForm

Out[2]//TraditionalForm=

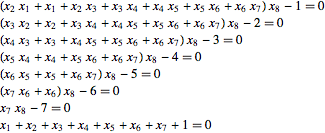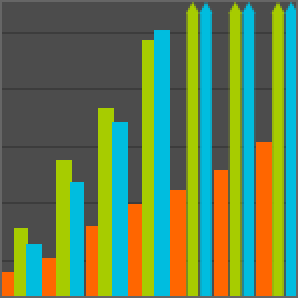
標準的なNoonburgのニューラルネットワーク系の比較は以下の式で与えられる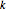． 個の変数の場合，この系は全次数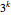，異なる解の数 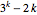である．

In[3]:=

X noon[k_] := Table[Subscript[x, i] (Sum[Subscript[x, j]^2, {j, 1, k}] - Subscript[x, i]^2 - 1.1) + 1 == 0, {i, 1, k}]

例えば5つの変数の場合，この系は次の形式を取る．

In[4]:=

X Column[noon[5]] // TraditionalForm

Out[4]//TraditionalForm=

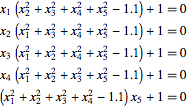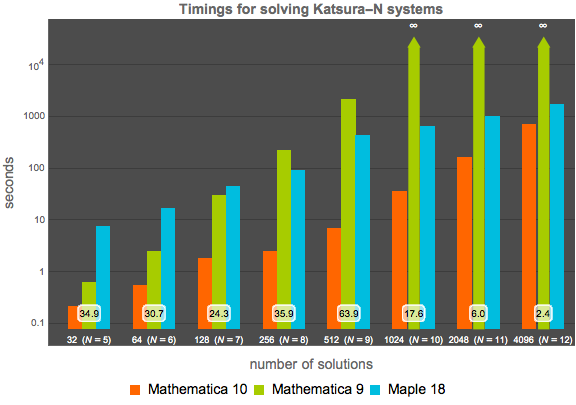
強磁性の格子確率の標準的なKatsura-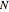 系の比較では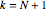，個の変数で全次数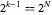と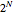個の異なる解を持つ．次数 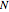の系では次の形式を取る．

In[5]:=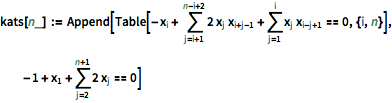

X kats[n_] := Append[Table[-Subscript[x, i] + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = i + 1\), \(n - i + 2\)]\(2\ \*SubscriptBox[\(x\), \(j\)]\ \*SubscriptBox[\(x\), \(i + j - 1\)]\)\) + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(i\)]\( \*SubscriptBox[\(x\), \(j\)]\ \*SubscriptBox[\(x\), \(i - j + 1\)]\)\) == 0, {i, n}], -1 + Subscript[x, 1] + \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 2\), \(n + 1\)]\(2\ \*SubscriptBox[\(x\), \(j\)]\)\) == 0]

例えば 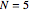の場合，この系には6つの未知数の6つの方程式がある．

In[6]:=

X Column[kats[5]] // TraditionalForm

Out[6]//TraditionalForm=
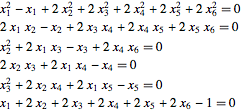