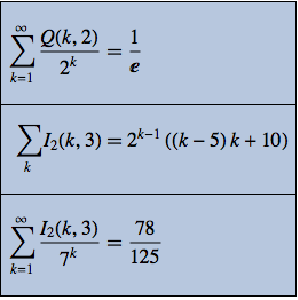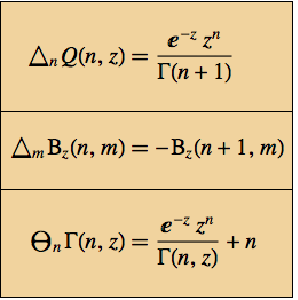DSolveValueを使って，常微分方程式の解に対する式を直接得る．
| In[1]:= |  X |
| Out[1]= |  |
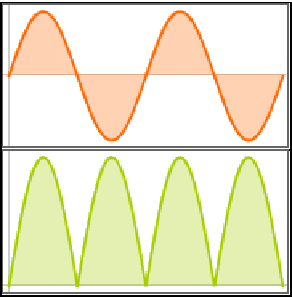
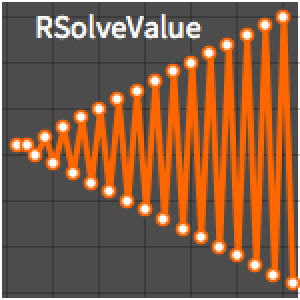
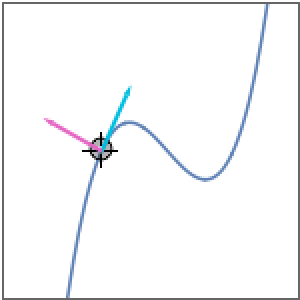
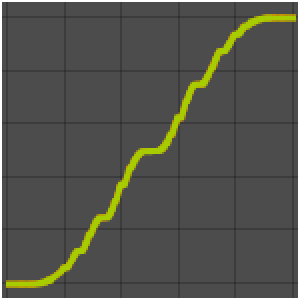
解をプロットする．
| In[2]:= |  X |
| Out[2]= |  |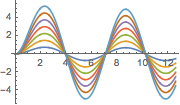
常微分方程式の解の導関数を計算する．
| In[3]:= |  X |
| Out[3]= |  |
従属変数を含む任意の式について解く．
| In[4]:= |  X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= | 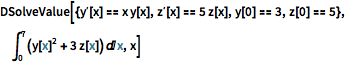 X |
| Out[6]= |  |
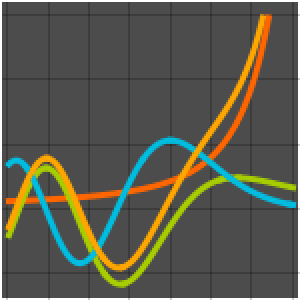
非線形の二階常微分方程式の純関数解を得る．
| In[7]:= |  X |
| In[8]:= |  X |
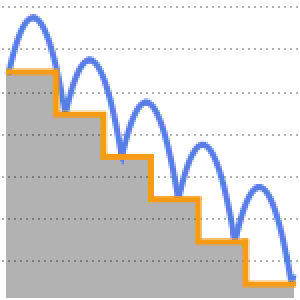
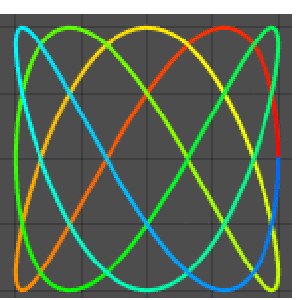
| Out[8]= |  |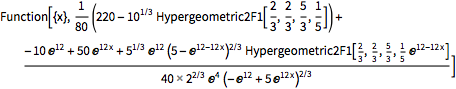
解を検証する．
| In[9]:= |  X |
| Out[9]= |  |
Compute Symbolic Solutions for ODEs with Events »
Directly Obtain Solution Expressions for ODEs »
Find Symbolic Solutions for Delay Differential Equations »
Automatically Invoke NDSolve if DSolve Fails »
Rectify a Periodic Wave »
Model a Ball Bouncing down Steps »
Design a Proportional-Derivative Controller »
Visualize Chaos in a Delay Differential Equation »
Evaluate New Classes of Telescoping Sums and Products »
Compute Sums Involving Special Functions »
Obtain Simple Differences and Ratios for Special Functions »
Directly Obtain Solution Expressions for Difference Equations »
Color a Curve by Arc Length »
Compute the Curvature of Curves in Any Dimensions »
Visualize the TNB Basis of a Knot »
Animate the Tangent and Normal to a Function »
Questions? Comments? Contact a Wolfram expert »
