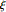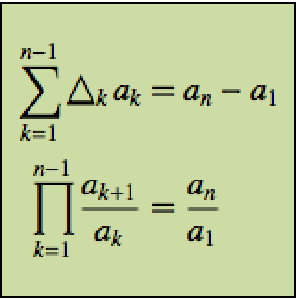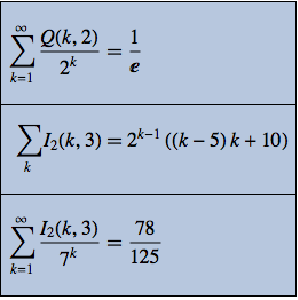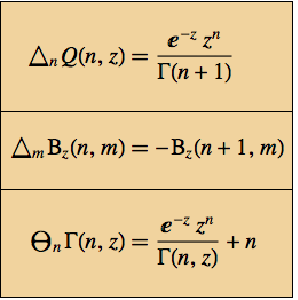增强的微积分和微分方程
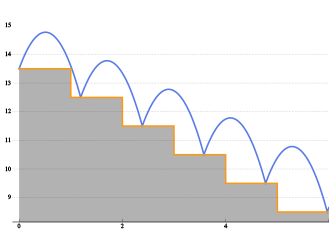
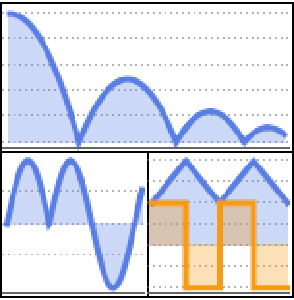
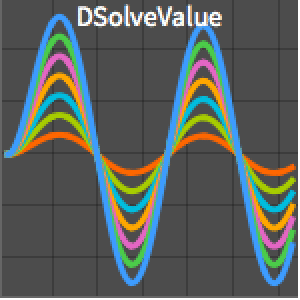
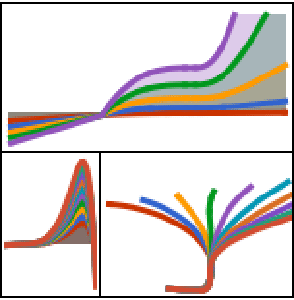
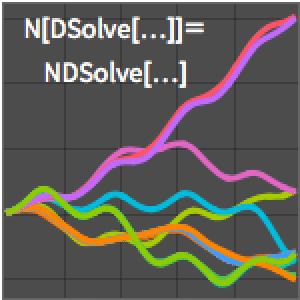
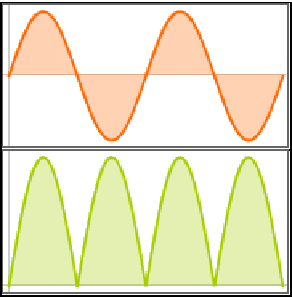
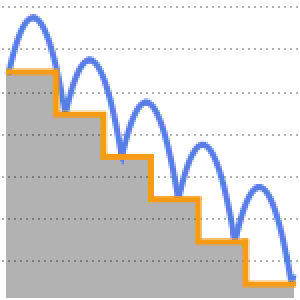
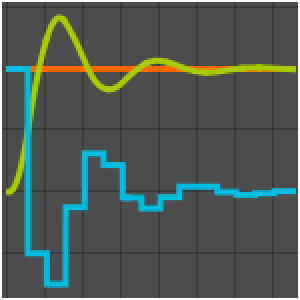
Version 10 adds many significant enhancements to its traditional strength in symbolic calculus. For the first time, symbolic solutions to hybrid differential equations with events and delay differential equations are possible. All discrete calculus operations are extended with newly developed algorithms motivated by probability and statistics. New dedicated commands for curve geometry as well as newly added special functions automate many tasks. Taken together, these developments will lead to smoother workflow for a wide range of applications, starting from college calculus to research level.