Use TransformedProcess to Create a Custom Process
Define compensated Poisson process.
| In[1]:= | X |
Simulate the process with unit rate for 30 seconds.
| In[2]:= | X |
| In[3]:= | X |
| Out[3]= | 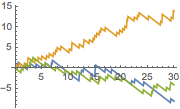 |
Compute the covariance function for the process.
| In[4]:= | X |
| Out[4]= |
Define a Bessel process in two dimensions.
| In[5]:= | 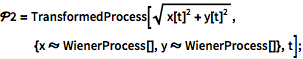 X |
Simulate the process for 10 seconds.
| In[6]:= | X |
| In[7]:= | X |
| Out[7]= | 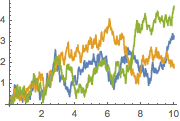 |
Compute the mean and variance functions for the process.
| In[8]:= | X |
| Out[8]= |
























