さまざまな性能の向上 

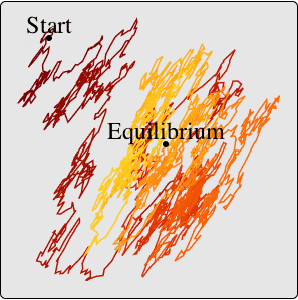
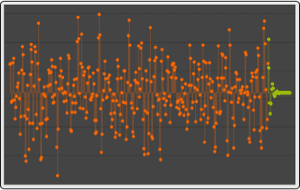
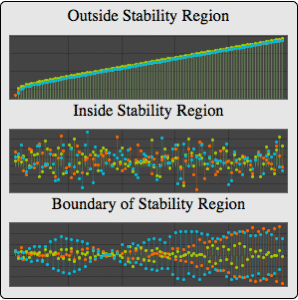
Mathematica 10では，サンプリング，共分散関数，対数尤度，スライスを含む線形時系列過程のサポートがさまざま面で向上している．

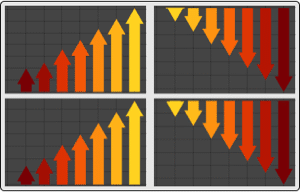
Mathematica 10，Mathematica 9，R 3.1.0において，スカラーARMA(2,1)過程の500経路のアンサンブルをサンプリングするのにかかる時間を経路長の関数として表す．この実験はIntel Core i7 2.93 GHzの64ビットWindowsシステムで行われた．棒の数字は Mathematica 10が Mathematica 9より何倍速いかを示している．

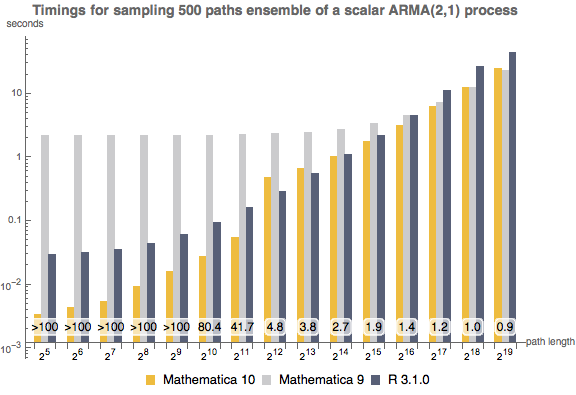Mathematica 10，Mathematica 9において，二次元ベクトルARMA(2,1)過程の50経路のアンサンブルをサンプリングするのにかかる時間を経路長の関数として表す．この実験はIntel Xeon 3.07 GHzの64ビットLinuxシステムで行われた．棒の数字は Mathematica 10が Mathematica 9より何倍速いかを示している．

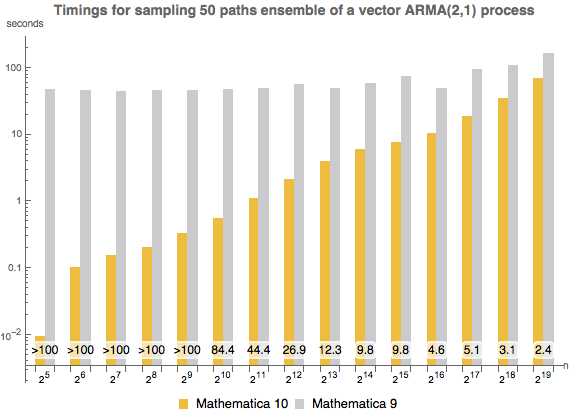Mathematica 10，Mathematica 9，R 3.1.0において，スカラーARMA(2,1)過程の自己共分散列の計算にかかる時間を最大遅延の関数として表す．この実験はIntel Core i7 2.93 GHzの64ビットWindowsシステムで120秒の時限制限付きで行われた．棒の数字は Mathematica 10が Mathematica 9より何倍速いかを示している．

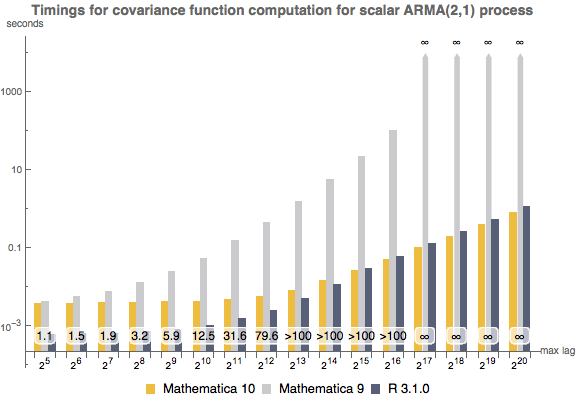Mathematica 10，Mathematica 9において，二次元ベクトルARMA(2,1)過程の自己共分散列の計算にかかる時間を最大遅延の関数として表す．この実験はIntel Xeon 3.07 GHzの64ビットLinuxシステムで行われた．棒の数字は Mathematica 10が Mathematica 9より何倍速いかを示している．
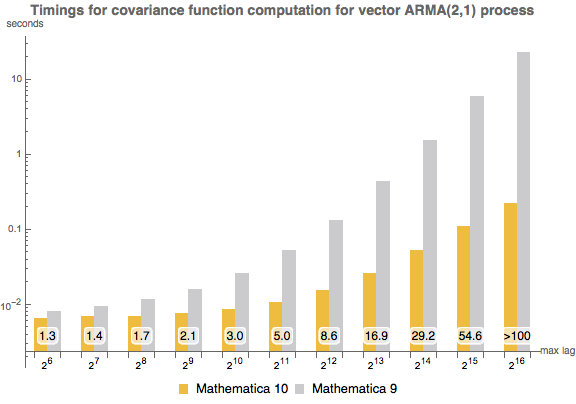