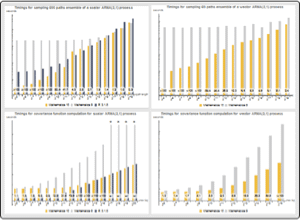
Vector Joint Model versus Univariate Component Models 

Get hourly temperature readings for May 2014 in Champaign, Illinois.

In[1]:=

X start = {2014, 5, 1, 0, 0, 0}; end = {2014, 5, 31, 23, 59, 0};

In[2]:=

X temp = WeatherData[{"Champaign", "IL"}, "Temperature", {start, end}]; temp1 = TimeSeries[temp, MissingDataMethod -> "Interpolation"]; temp2 = TimeSeriesResample[temp1, "Hour"];

Use TimeSeriesAggregate to calculate daily minimum and maximum temperatures.

In[3]:=

X min = TimeSeriesAggregate[temp2, "Day", Min]; max = TimeSeriesAggregate[temp2, "Day", Max];

Combine them into a vector time series.

In[4]:=

X dataAll = TimeSeries[TimeSeriesThread[QuantityMagnitude, {min, max}], MetaInformation -> {"Units" -> {"DegreesCelsius", "DegreesCelsius"}, "Observation" -> {"Min Temperature", "Max Temperature"}}]

Out[4]=

show complete Wolfram Language inputhide input

In[5]:=

X Table[DateListPlot[dataAll["PathComponent", i], FrameLabel -> {None, dataAll["Units"][[i]]}, PlotLabel -> dataAll["Observation"][[i]], ImageSize -> 250, PlotTheme -> "Detailed"], {i, 2}]

Out[5]=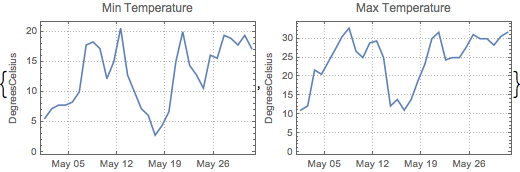

The first part of the data will be used to find a model, while the rest of the data will serve as a reference set for the forecast.

In[6]:=

X data = TimeSeriesWindow[ dataAll, {Automatic, {2014, 5, 26, 23, 59, 0}}];

The temperatures are cross-correlated.

In[7]:=

X ListPlot[TimeSeriesMap[Part[#, 1, 2] &, CorrelationFunction[data, {20}]], Filling -> Axis]

Out[7]=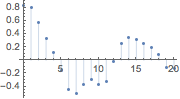

Fit a vector model to the data.

In[8]:=

X model[p_, q_] := ARIMAProcess[p, q]; eproc = EstimatedProcess[data, model[1, 0]]

Out[8]=

Forecast the next 5 days.

In[9]:=

X n = 5; forecast = TimeSeriesForecast[eproc, data, {n}, Method -> "Covariance"];

show complete Wolfram Language inputhide input

In[10]:=

X Table[DateListPlot[{dataAll["PathComponent", i], forecast["PathComponent", i]}, FrameLabel -> {None, data["Units"][[i]]}, PlotLabel -> data["Observation"][[i]], ImageSize -> 250, PlotRange -> All, PlotTheme -> "Detailed"], {i, 2}]

Out[10]=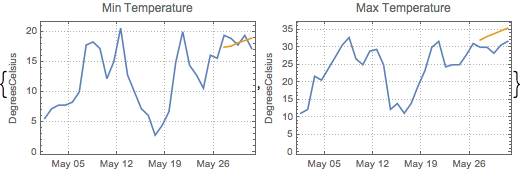

Find univariate models of the same type but longer orders for both temperatures separately.

In[11]:=

X minProc = EstimatedProcess[data["PathComponent", 1], model[3, 0]] minForecast = TimeSeriesForecast[minProc, data["PathComponent", 1], {n}, Method -> "Covariance"];

Out[11]=

In[12]:=

X maxProc = EstimatedProcess[data["PathComponent", 2], model[3, 0]] maxForecast = TimeSeriesForecast[maxProc, data["PathComponent", 2], {n}, Method -> "Covariance"];

Out[12]=

Combine univariate forecasts for plotting.

In[13]:=

X uForecast = TimeSeries[ Transpose@{minForecast["Values"], maxForecast["Values"]}, {minForecast["Dates"]}]

Out[13]=

Compare the forecasts.

In[14]:=

X plotData = TimeSeriesWindow[dataAll, {"May 20, 2014", Automatic}];

show complete Wolfram Language inputhide input

In[15]:=

X Legended[Row@ Table[DateListPlot[{plotData["PathComponent", i], forecast["PathComponent", i], uForecast["PathComponent", i]}, ImageSize -> 250, PlotTheme -> "Detailed", PlotLabel -> dataAll["Observation"][[i]]], {i, 1, 2}], Placed[SwatchLegend[{RGBColor[0.368417, 0.506779, 0.709798], RGBColor[0.880722, 0.611041, 0.142051], RGBColor[ 0.560181, 0.691569, 0.194885]}, {"data ", "forecast with a vector model", "forecast with an univariate model"}, LegendLayout -> "Row"], Below]]

Out[15]=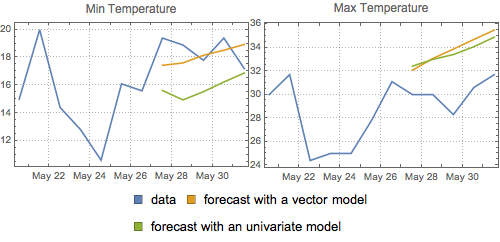

Plot the vector forecast and the 95% confidence bands.

show complete Wolfram Language inputhide input

In[16]:=

X nq = Quantile[NormalDistribution[], 0.975]; ubandV = Table[ TimeSeriesThread[{1, nq}.# &, {forecast["PathComponent", i], TimeSeriesMap[Sqrt[#[[i, i]]] &, forecast["MeanSquaredErrors"]]}], {i, 1, 2}]; lbandV = Table[ TimeSeriesThread[{1, -nq}.# &, {forecast["PathComponent", i], TimeSeriesMap[Sqrt[#[[i, i]]] &, forecast["MeanSquaredErrors"]]}], {i, 1, 2}];

In[17]:=

X pV = Table[ DateListPlot[{plotData["PathComponent", i], forecast["PathComponent", i], ubandV[[i]], lbandV[[i]]}, PlotStyle -> {Automatic, RGBColor[0.880722, 0.611041, 0.142051], Brown, Brown}, PlotRange -> All, Filling -> {3 -> {4}, 6 -> {7}}, PlotTheme -> "Detailed", PlotLabel -> dataAll["Observation"][[i]], ImageSize -> 250], {i, 1, 2}]; Legended[Row[pV], Placed[SwatchLegend[{RGBColor[0.368417, 0.506779, 0.709798], RGBColor[0.880722, 0.611041, 0.142051], Brown}, {"data ", "vector forecast"}, LegendLayout -> "Row"], Bottom]]

Out[17]=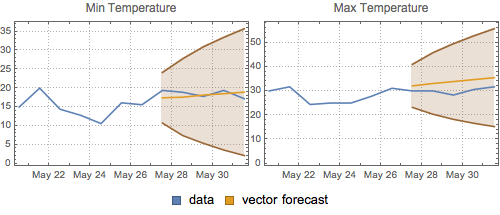

Plot the univariate forecasts and the 95% confidence bands.

show complete Wolfram Language inputhide input

In[18]:=

X err = {minForecast["MeanSquaredErrors"], maxForecast["MeanSquaredErrors"]};

In[19]:=

X nq = Quantile[NormalDistribution[], 0.975]; ubandU = Table[ TimeSeriesThread[{1, nq}.# &, {uForecast["PathComponent", i], TimeSeriesMap[Sqrt, err[[i]]]}], {i, 1, 2}]; lbandU = Table[ TimeSeriesThread[{1, -nq}.# &, {uForecast["PathComponent", i], TimeSeriesMap[Sqrt, err[[i]]]}], {i, 1, 2}];

In[20]:=

X pU = Table[ DateListPlot[{plotData["PathComponent", i], uForecast["PathComponent", i], ubandU[[i]], lbandU[[i]]}, PlotStyle -> {Automatic, RGBColor[0.560181, 0.691569, 0.194885], Gray, Gray}, PlotRange -> All, Filling -> {3 -> {4}, 6 -> {7}}, PlotTheme -> "Detailed", PlotLabel -> dataAll["Observation"][[i]], ImageSize -> 250], {i, 1, 2}]; Legended[Row[pU], Placed[SwatchLegend[{RGBColor[0.368417, 0.506779, 0.709798], RGBColor[0.560181, 0.691569, 0.194885], Gray}, {"data ", "univariate forecast"}, LegendLayout -> "Row"], Bottom]]

Out[20]=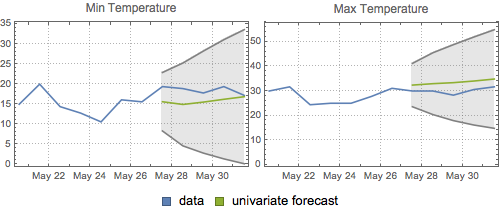

Compare both forecasts and the corresponding confidence bands.

show complete Wolfram Language inputhide input

In[21]:=

X Legended[Grid[{First /@ {pV, pU}, Last /@ {pV, pU}}], Placed[SwatchLegend[{RGBColor[0.368417, 0.506779, 0.709798], RGBColor[0.880722, 0.611041, 0.142051], RGBColor[ 0.560181, 0.691569, 0.194885]}, {"data ", "forecast with a vector model", "forecast with an univariate model"}, LegendLayout -> "Row"], Below]]

Out[21]=