Investigate Time Series Model Residuals
Having found the model that successfully describes the time series of interest, the fit residual is expected to be a Gaussian white noise process.
Monthly data of accidental deaths in USA from 1973 to 1978.
| In[1]:= | X |
| In[2]:= | X |
| Out[2]= |  |
Fit an ARMA model to the data.
| In[3]:= | X |
| Out[3]= |  |
Autocorrelation, partial autocorrelation, and Ljung–Box plots suggest correlation at lag 12.
| In[4]:= | X |
| Out[4]= | 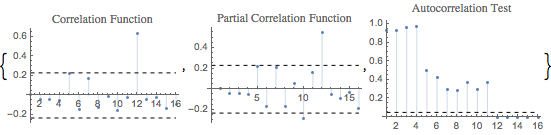 |
Fit a seasonal ARMA model with seasonality of 12.
| In[5]:= | X |
| Out[5]= |  |
ACF, PACF, and Ljung–Box plots indicate that residuals are likely a white noise.
| In[6]:= | X |
| Out[6]= | 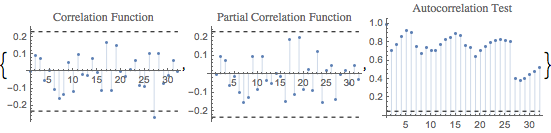 |
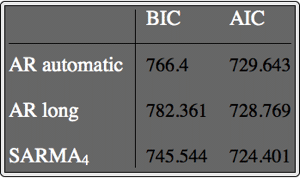
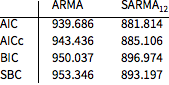
Selection criteria favor the seasonal model over the non-seasonal one.
| In[7]:= |  X |
| Out[7]//TableForm= | |
 | |