Vector Autoregressive Process as Discretized Vector Ornstein–Uhlenbeck Process 

Improved support for computation with process slices, as well as support for arbitrary mean time series processes and time processes with initial values, allows the matching of a uniformly discretized Gaussian Ito process to a vector-valued autoregressive process.

Define a 2D Ito process with linear drift coefficients and constant diffusion coefficients.

In[1]:=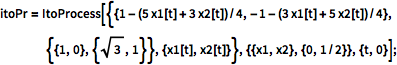

X itoPr = ItoProcess[{{1 - (5 x1[t] + 3 x2[t])/ 4, -1 - (3 x1[t] + 5 x2[t])/4}, {{1, 0}, {Sqrt[3], 1}}, {x1[t], x2[t]}}, {{x1, x2}, {0, 1/2}}, {t, 0}];

Define a bivariate autoregressive process with initial values.

In[2]:=

X varPr = ARProcess[{c1, c2}, {{{a11, a12}, {a21, a22}}}, {{s1, s12}, {s12, s2}}, {{x10ar, x20ar}}];

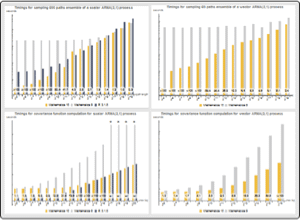
Since both processes are Gaussian, they are completely specified by their mean and covariance functions.

In[3]:=

X itoPrmf[t_] = Mean[itoPr[t]];

In[4]:=

X itoPrcovF[s_, t_] = Simplify[CovarianceFunction[itoPr, s, t]];

In[5]:=

X varPrmf[n_] = Mean[varPr[n]];

In[6]:=

X varPrcovF[n_, m_] = Simplify[CovarianceFunction[varPr, n, m]];

Construct equations of moments by equating the Ito process moment functions at regularly spaced times and the VAR moment functions at consecutive integers.

In[7]:=

X dt = 1/1000;

In[8]:=

X meanEqs = Table[itoPrmf[n dt] == varPrmf[n - 1], {n, 4}]; covEqs = Table[ Flatten[itoPrcovF[n dt, m dt]] == Flatten[varPrcovF[n - 1, m - 1]], {n, 4}, {m, n, 4}];

Solve the equations.

In[9]:=

X {sol} = NSolve[ Join[meanEqs, Flatten[covEqs]], {c1, c2, x10ar, x20ar, a11, a12, a21, a22, s1, s2, s12}]

Out[9]=

Simulation of the VAR process gives exact simulation of the Ito process of the regular grid.

In[10]:=

X path = RandomFunction[varPr /. sol, {0, 20000}]

Out[10]=

Visualize the path.

show complete Wolfram Language inputhide input

In[11]:=

X Legended[Graphics[{{Gray, Line[path["Values"]]}, {Red, PointSize[.03], Point[{x10ar, x20ar} /. sol]}, {Orange, PointSize[.03], Point[Limit[itoPrmf[t], t -> Infinity]]} }, AspectRatio -> 1, Frame -> True, ImageSize -> Medium], LineLegend[{Red, Orange, Gray}, {"starting point", "stationary mean", "process path"}, Joined -> {False, False, True}]]

Out[11]=