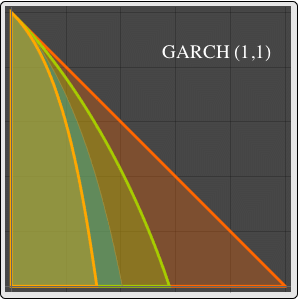
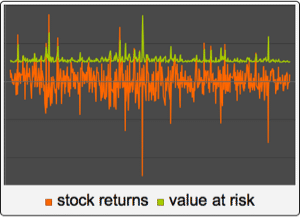
Volatility Clustering in a GARCHProcess 

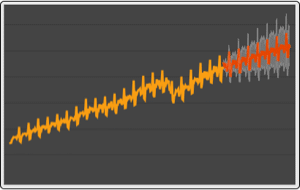
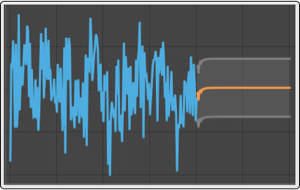
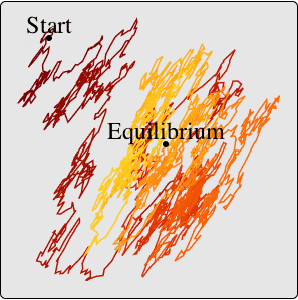
Generalized autoregressive conditionally heteroscedastic process GARCHProcess is used to describe time series that exhibit volatility clustering phenomenon—large changes tend to be followed by large changes of either sign, and small changes tend to be followed by small changes.

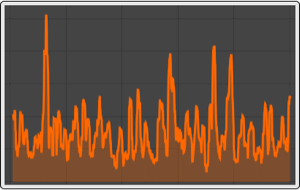
Simulate a GARCHProcess.

In[1]:=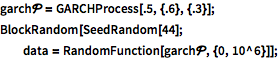

X garch\[ScriptCapitalP] = GARCHProcess[.5, {.6}, {.3}]; BlockRandom[SeedRandom[44]; data = RandomFunction[garch\[ScriptCapitalP], {0, 10^6}]];

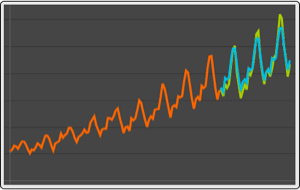
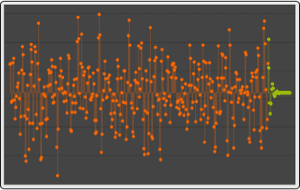
Plot moving standard deviation with window of length 10.

In[2]:=

X var = MovingMap[StandardDeviation, data, 10]; ListLinePlot[TimeSeriesResample[var, 100], PlotRange -> {0, 40}, Ticks -> {Table[{10^5 k, k}, {k, 10}], Automatic}, AxesLabel -> {"\[Times] 10^5", None}, ImageSize -> Medium]

Out[2]=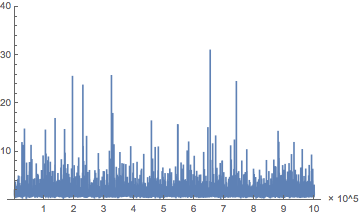

Define a function to compute standard deviation, given that the previous time value of the process is close to a given number.

show complete Wolfram Language inputhide input

In[3]:=

X cfBinarySearch = Compile[{{list, _Real, 1}, {elem, _Real}}, Module[{n0 = 1, n1 = Length[list], m = 1, lm}, While[n0 < n1, m = Quotient[n0 + n1, 2]; lm = Part[list, m]; If[lm == elem, Break[]]; If[lm < elem, n0 = m + 1, n1 = m - 1]]; m], RuntimeOptions -> "Speed", RuntimeAttributes -> Listable];

In[4]:=

X condVar[pd_, v_] := Module[{cd, n, var, p0, p1}, {p0, p1} = cfBinarySearch[pd[[All, 1]], v + Abs[v] {-0.1, 0.1}]; cd = Take[pd, {p0 - 1, p1}]; n = Length[cd]; If[n > 10, {Mean[cd[[All, 1]]], StandardDeviation[cd[[All, 2]]]}, {Indeterminate, Indeterminate}]]

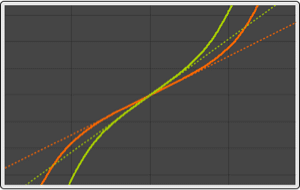
Estimate conditional standard deviation as a function of the conditional value.

In[5]:=

X Quantile[data, {0, 0.01, 0.05, 0.95, 0.99, 1}]

Out[5]=

In[6]:=

X vlist = Join[#, -#] &[{1, 2, 4, 6, 8, 10, 15, 20, 25, 30, 35, 40}]; Block[{pd = SortBy[Partition[data["Values"], 2, 1], First]}, sdEst = Table[condVar[pd, v], {v, Sort[vlist]}]];

In[7]:=

X ListLinePlot[SortBy[sdEst, First]]

Out[7]=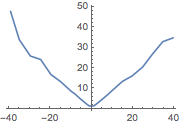

Compare to the graph for a sample of an ARMA process, whose conditional standard deviation is constant.

In[8]:=

X arma\[ScriptCapitalP] = ARMAProcess[{.6, 0.1}, {.3}, 1]; BlockRandom[SeedRandom[44]; data2 = RandomFunction[arma\[ScriptCapitalP], {10^6}]];

In[9]:=

X Quantile[data2, {0, 0.01, 0.05, 0.25, 0.75, 0.95, 0.99, 1}]

Out[9]=

In[10]:=

X vlist = Join[#, -#] &[{0.5, 1, 2, 3, 4, 5}]; Block[{pd2 = SortBy[Partition[data2["Values"], 2, 1], First]}, sdEst2 = Table[condVar[pd2, v], {v, Sort[vlist]}]];

In[11]:=

X ListLinePlot[SortBy[sdEst2, First], PlotRange -> {0, 2}]

Out[11]=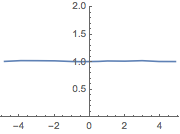