Moments of GARCH(1,1) 

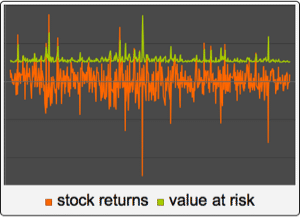
The value of a generalized autoregressive conditionally heteroscedastic process GARCHProcess has a heavy-tailed distribution with only a few finite moments of low order.

Fourth moment of a GARCHProcess with orders (1,1).

In[1]:=

X Moment[GARCHProcess[k, {a}, {b}][t], 4]

Out[1]=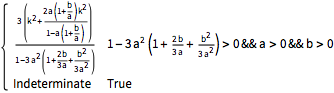

Define the function to extract moment finiteness conditions.

In[2]:=

X mc[r_] := Reduce[Exists[{k, t}, {t, k} \[Element] Reals, Moment[GARCHProcess[k, {a}, {b}][t], r] \[Element] Reals], {a, b}]

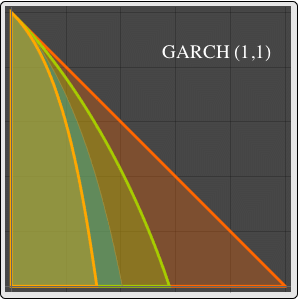
Visualize the parameter conditions for moments to exist.

In[3]:=

X orders = {2, 4, 6, 8}; RegionPlot[Evaluate@Table[mc[r], {r, orders}], {a, 0, 1}, {b, 0, 1}, PlotLegends -> (Row[{"r = ", #}] & /@ orders), FrameLabel -> Automatic]

Out[3]=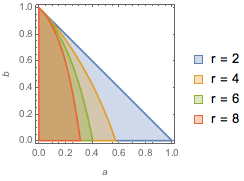

Values of the first few even moments for a weakly stationary GARCHProcess.

show complete Wolfram Language inputhide input

In[4]:=

X lg3 = Log10[3.]; ticks = {Automatic, {{lg3, 3}, {1, 10}, {lg3 + 1, 30}, {2, 100}, {lg3 + 2, 300}, {3, 1000}}};

In[5]:=

X DiscretePlot[ Log10[Moment[GARCHProcess[.3, {.2}, {.3}][t], r]], {r, 0, 10, 2}, ExtentSize -> 1/2, PlotTheme -> "Grid", Ticks -> ticks]

Out[5]=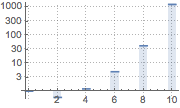

Compare to the values of the even moments for a non-weakly stationary GARCH with process initial values set to zero.

In[6]:=

X Grid[Partition[ Table[DiscretePlot[ Log10[Moment[GARCHProcess[.3, {.2}, {.3}, {}][t], r]], {r, 0, 10, 2}, ExtentSize -> 1/2, PlotTheme -> "Grid", Ticks -> ticks, PlotRange -> {-1, 4}, PlotLabel -> Row[{"t = ", t}]], {t, 1, 4}], 2]]

Out[6]=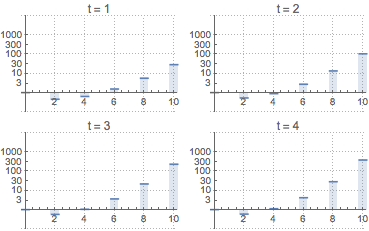