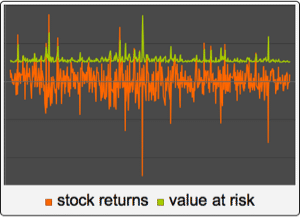
Study Significance of Parameters in Fitted Model
The estimated parameters of the model may be small—smaller than the expected estimator variance. This may indicate a need to use a simpler or more structured model.
Get a random sample by applying a moving average filter to a white noise signal.
| In[1]:= |  X |
| Out[1]= |
Fit zero mean time series model to data.
| In[2]:= | X |
| Out[2]= | 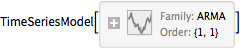 |
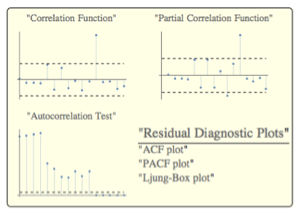
Show parameter tables, displaying the estimated time series parameters and their standard deviations, as well as the corresponding 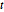 -test statistics and
-test statistics and 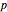 -value.
-value.
| In[3]:= | X |
| Out[3]= |  |
The parameter table indicates that autoregressive coefficient 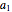 is not significantly different from zero. Find the maximum likelihood estimate of the MA(1) model.
is not significantly different from zero. Find the maximum likelihood estimate of the MA(1) model.
| In[4]:= | X |
| Out[4]= |
The Akaike information criterion favors the MLE estimated MA(1) model.
| In[5]:= | X |
| Out[5]= |
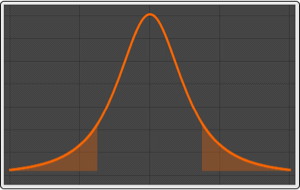
Compute the 95% confidence interval of the moving-average parameter.
| In[6]:= | X |
| Out[6]= |