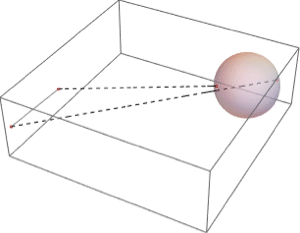
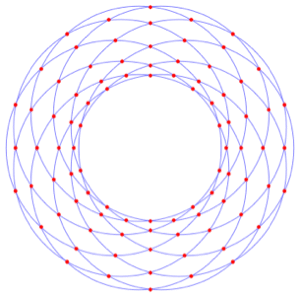
派生領域 

派生領域は，他の領域から構築された領域である．その典型的な例として，他の領域のブール結合，他の領域の変換，領域の直積を使うものが含まれる．派生領域では領域をステップごとに増加させて構築することが可能である．Wolfram言語では，派生領域は領域を厳密にも近似的にも表現することができる．

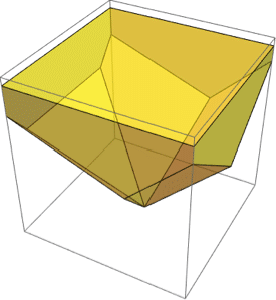
領域のブール結合．

In[1]:=

X r1 = Disk[{-1/2, 0}]; r2 = Disk[{1/2, 0}];

In[2]:=

X d1 = RegionUnion[r1, r2]; d2 = RegionIntersection[r1, r2]; d3 = RegionDifference[r1, r2]; d4 = RegionSymmetricDifference[r1, r2];

In[3]:=

X Table[Show[BoundaryDiscretizeRegion[r], PlotRange -> {{-1.65, 1.65}, {-1.1, 1.1}}, PlotLabel -> Head[r]], {r, {d1, d2, d3, d4}}]

Out[3]=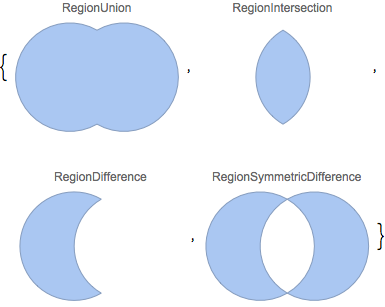

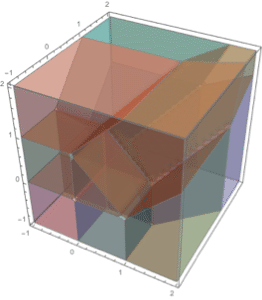
領域の変換．

In[4]:=

X r = DiscretizeGraphics[Cuboid[]]

Out[4]=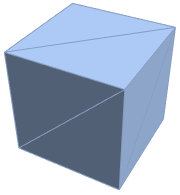

In[5]:=

X t1 = ScalingTransform[{2, 1, 1}]; t2 = RotationTransform[\[Pi]/3, {1, 1, 1}]; t3 = ShearingTransform[\[Pi]/6, {1, 1, 0}, {0, 0, 1}]; t4 = Composition[t3, t2, t1];

In[6]:=

X Table[TransformedRegion[r, t], {t, {t1, t2, t3, t4}}]

Out[6]=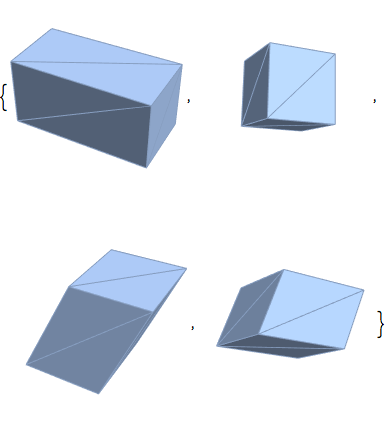

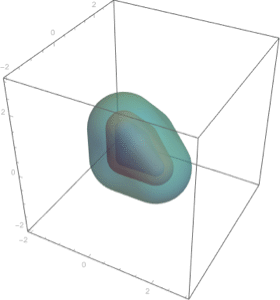
領域の直積．

In[7]:=

X CantorLine[n_Integer?NonNegative] := Module[{ints, cantor = {a_, b_} :> {{a, a + (b - a)/3}, {a + (b - a) 2/3, b}}}, ints = Nest[ Flatten[Map[Function[s, s /. cantor], #], 1] &, {{0, 1}}, n]; MeshRegion[Transpose[{Flatten[ints]}], Line@Table[{i, i + 1}, {i, 1, Length[ints] 2, 2}]]]

In[8]:=

X Table[CantorLine[k], {k, 0, 3}]

Out[8]=

In[9]:=

X RegionProduct[CantorLine[3], CantorLine[3]]

Out[9]=

In[10]:=

X RegionProduct[CantorLine[3], CantorLine[3], CantorLine[3]]

Out[10]=