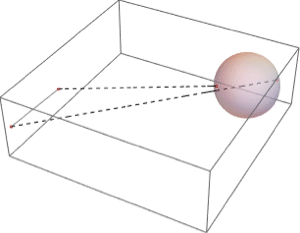
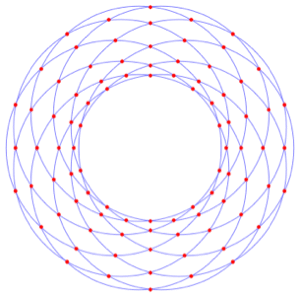
領域上で方程式を解く
領域制約を持つ方程式および不等式を解く．領域制約は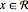 
を使って表され，他の制約条件と一緒に使うことができる．大域的な数値方程式ソルバの他，記号的な方程式ソルバもこの新しい制約条件をサポートする．
2つの無限直線の交点を求める．
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= |  |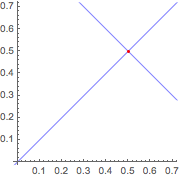
直線と円の交点を厳密に求める．
| In[4]:= |  X |
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= |  X |
| Out[6]= |  |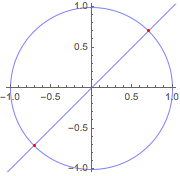
同じ問題を解くのに記号的ベクトル変数を使う．
| In[7]:= |  X |
| In[8]:= |  X |
| Out[8]= |  |
| In[9]:= |  X |
| Out[9]= |  |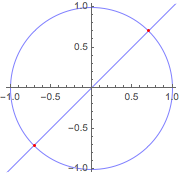
与えられた円の集合に対して，円と円の交点をすべて求める．
| In[10]:= |  X |
| In[11]:= |  X |
| Out[11]= |  |
| In[12]:= |  X |
| Out[12]= |  |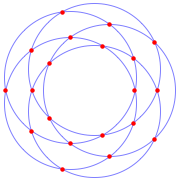
3つの球が交わる点を見付ける．
| In[13]:= |  X |
| In[14]:= |  X |
| Out[14]= |  |
| In[15]:= |  X |
| Out[15]= |  |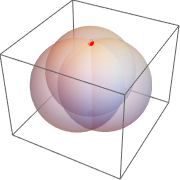
