Solve Equations over Regions
Solve equations and inequalities with region constraints. Region constraints are expressed using 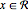 and can be used together with other constraints. Symbolic equation solvers as well as global numeric equation solvers support these new constraints.
and can be used together with other constraints. Symbolic equation solvers as well as global numeric equation solvers support these new constraints.
Find the intersection of two infinite lines.
| In[1]:= | X |
| In[2]:= | X |
| Out[2]= |
| In[3]:= | X |
| Out[3]= | 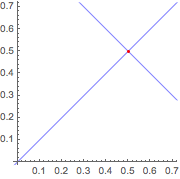 |
Find the intersections between a line and a circle exactly.
| In[4]:= | X |
| In[5]:= | X |
| Out[5]= |
| In[6]:= | X |
| Out[6]= | 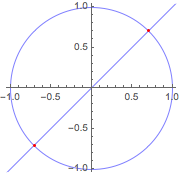 |
Use symbolic vector variables to solve the same problem.
| In[7]:= | X |
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= | 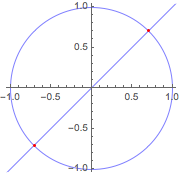 |
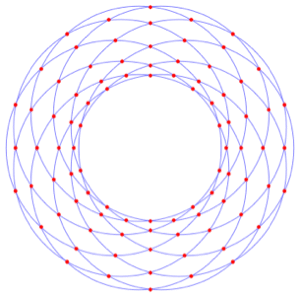
Find all pairwise intersections of the given circles.
| In[10]:= | X |
| In[11]:= | X |
| Out[11]= |  |
| In[12]:= | X |
| Out[12]= | 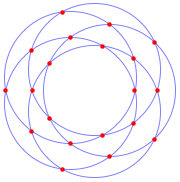 |
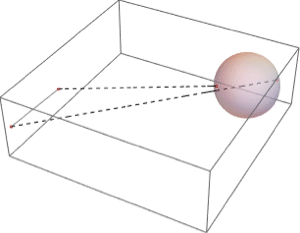
Find the points where three spheres intersect.
| In[13]:= | X |
| In[14]:= | X |
| Out[14]= |
| In[15]:= | X |
| Out[15]= | 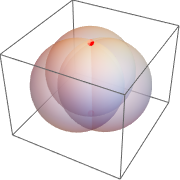 |