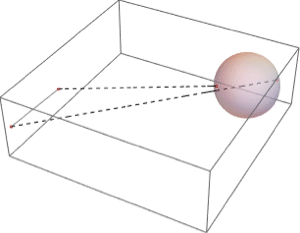
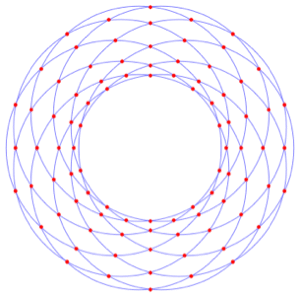
在区域上解方程式
使用区域约束求解方程和不等式. 用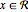 
表示区域约束，它可以和其他约束一起使用. 符号式方程式求解器以及全局数值方程求解器支持这些新的约束.
找出两条无限长线的交点.
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= |  |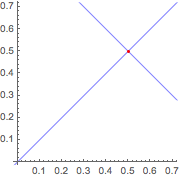
求直线和圆的确切交点.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= |  X |
| Out[6]= |  |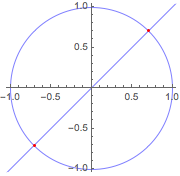
使用符号向量变量解答相同问题.
| In[7]:= |  X |
| In[8]:= |  X |
| Out[8]= |  |
| In[9]:= |  X |
| Out[9]= |  |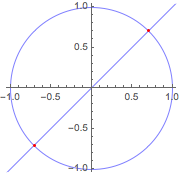
找出给定圆的全部成对交点.
| In[10]:= |  X |
| In[11]:= |  X |
| Out[11]= |  |
| In[12]:= |  X |
| Out[12]= |  |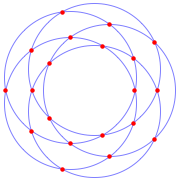
找出三个球体的交点.
| In[13]:= |  X |
| In[14]:= |  X |
| Out[14]= |  |
| In[15]:= |  X |
| Out[15]= |  |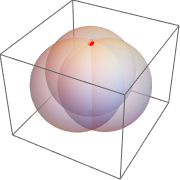
