在区域上解偏微分方程
在一维、二维和三维等全维区域数值求解偏微分方程. 使用的方法主要是基于有限元以及狄利克雷、诺伊曼、Robin 边界条件和时变方程.
在零边界条件的圆盘上解泊松方程 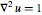 .
.
| In[1]:= | X |
| Out[1]= |  |
| In[2]:= | X |
| Out[2]= | 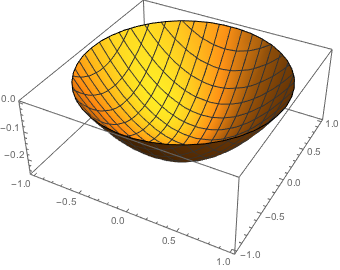 |
在更复杂的区域上解泊松方程 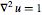 .
.
| In[3]:= |  X |
| In[4]:= | X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= | 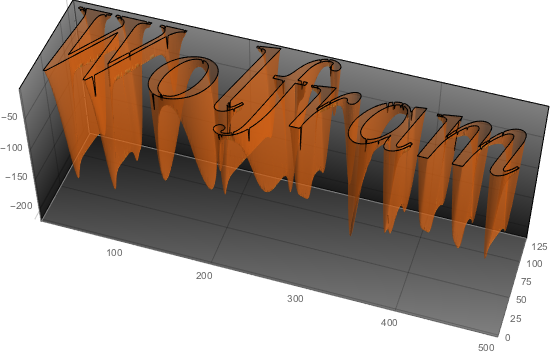 |
在一维、二维和三维等全维区域数值求解偏微分方程. 使用的方法主要是基于有限元以及狄利克雷、诺伊曼、Robin 边界条件和时变方程.
在零边界条件的圆盘上解泊松方程 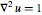 .
.
| In[1]:= | X |
| Out[1]= |  |
| In[2]:= | X |
| Out[2]= |  |
在更复杂的区域上解泊松方程 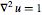 .
.
| In[3]:= |  X |
| In[4]:= | X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= |  |
Questions? Comments? Contact a Wolfram expert »