領域上で偏微分方程式を解く
1D，2D，3Dの全次元領域上で数値的に偏微分方程式を解く．使用されるメソッドは基本的に有限要素に基づき，時変形方程式の他ディリクレ(Dirichlet)，ノイマン(Neumann)，ロビン(Robin)の境界条件が使える．
円板上で，ゼロ境界条件のポワソン(Poisson)方程式
を解く．
| In[1]:= |  X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= |  |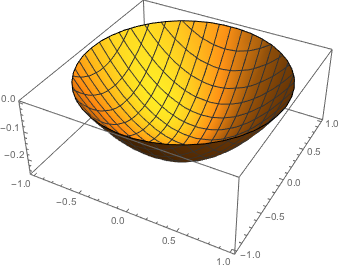
より複雑な領域上でポワソン方程式
を解く．
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= |  |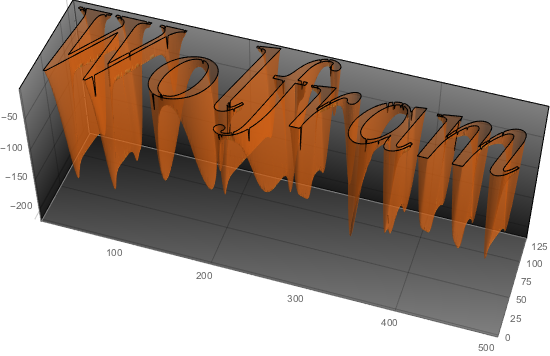
