Solve Partial Differential Equations over Regions
Solve partial differential equations numerically over full-dimensional regions in 1D, 2D, and 3D. The method used is primarily based on finite elements and allows for Dirichlet, Neumann, and Robin boundary conditions, as well as time-varying equations.
Solve a Poisson equation 
over a disk and with zero boundary conditions.
| In[1]:= |  X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= |  |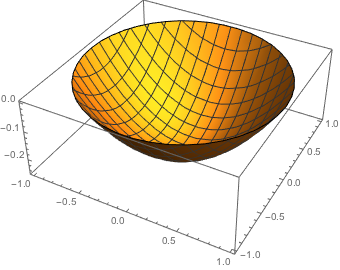
Solve a Poisson equation 
over a more complicated region.
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= |  |
