離散微積分

Mathematica が1988に最初にリリースされたとき，Mathematica の最大の功績の一つは従来の微積分を自動化したことであった．アルゴリズム的開発の大きな功績として，Mathematica 7は今回システム的な自動化を離散微積分にもたらした．さまざまな分野における100年以上に渡る異種の結果に注目して，Wolfram Researchにおける長期の研究開発は，今回初めて離散微積分の一貫したアルゴリズム的取扱いを可能にするような革新をもたらしたのである．この成果により，金融，保険数理，統計，組合せ論，アルゴリズム解析，情報理論，数値分析，統計物理学，制御論，信号処理等の分野における離散問題に対する新しく効率的な取扱いを即座に可能にした．

任意次数の有限差分，割合，転換の完全な記号的サポート »
100を超える新しい種類の記号的な和と積を網羅する主要アルゴリズム
無限および多変量の和と積をサポート »
多くの新しい種類の関数型および差分の方程式の記号解 »
常差分方程式，偏差分方程式，差分代数方程式に対する新たなアルゴリズム
すべての種類の差分方程式に対する最適化された数値解
多変量のものを含めた普通の指数母関数のサポート »
完全な多変量のZ変換，離散時間フーリエ（Fourier）変換，およびディリクレ（Dirichlet）変換 »
新しい離散たたみ込み，ディリクレのたたみ込み，および約数和関数 »
新しい記号的な連分数の演算子 »
和の収束の記号的条件を決定する関数 »
系統だった恒等式証明を含めた，ホロノミックな数列へのサポート
閉形と母関数を求めるための数列認識 »
アーベル(Abel)，ボレル(Borel)，チェザロ(Cesàro)および発散和のための他の正規化メソッドをサポート »
離散微積分を通してq関数を完全サポート »
カゾラティ(Casorati)の線形独立性検証 »
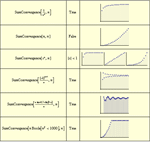
離散関数の可視化を直接サポート »


連続および離散の微積分アナログ	無限和のギャラリーを生成する	有限和の集合を計算する

多変量和を探究する	無限積と有限積のサンプルを取る	記号的なZ変換を生成する

記号的な母関数を求める	新しい種類の関数型方程式を解く	総和の入力の完全な型を探究する

無限級数の収束を調べる	発散の和と積を正規化する	区分数列の和を求める

記号的な連分数を計算する	アルゴリズムの複雑性を分析する	記号的な差分を計算する

記号的な離散率のサンプルを取る	q関数を離散微積分に適用する	離散化偏微分方程式を解く

階乗ベキ級数近似を計算する	イベントに対する確率を計算する	非同次の常微分方程式のパラメータの変化を適用する

その他