Examples
1. Statics
In statics, we input and output forces (including gravitational forces on any mass present).
Example - Force and Spring Equilibrium
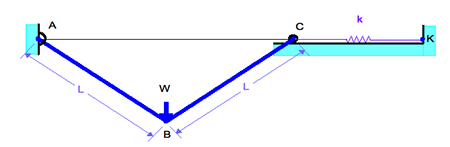
A vertical load W is applied to the linkage shown at B. The spring is unstretched when the bars are horizontal. Find an expression for the equilibrium position of the linkage.
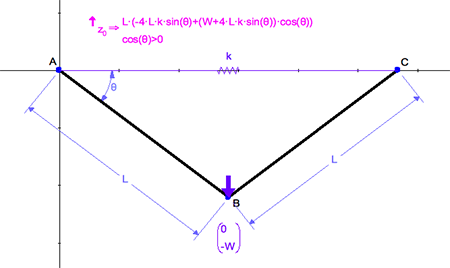
Our model mounts the spring between A and C and uses a free length of 2*L. An expression for equilibrium may be derived by equating the reaction in angle θ to 0.
Notes:
-
Check the value of W in the Variables panel. Make sure it is positive. If W has a negative value, the Applied Force arrow will point in the opposite direction, as the y value of the vector is -W.
- In this example, we did not use a damping coefficient or actuator force, so make sure the Enabled checkboxes for these sections in the Spring Parameters dialog are unchecked.
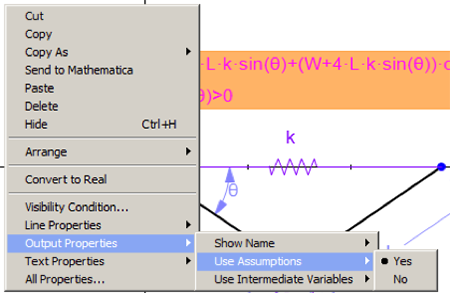
- To be sure you have the simplest output expression in θ, select the output and right-click to get the Context menu. Select Output Properties / Use Assumptions / Yes. This option can also be set in the Edit / Preferences dialog in the Math tab.
2. Kinematics
In kinematics, we input and output velocity and acceleration.
Example - Force and Spring Equilibrium
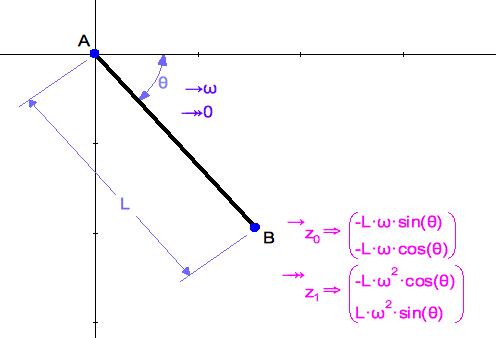
Here is a model of a pendulum with a given angular velocity applied to the angle θ. The velocity and acceleration of point B are measured in terms of ω.
3. Kinetostatics
In kinetostatics, we have input force elements and velocity/acceleration elements, and output force elements.
Masses acquire not only body force due to gravity, but force due to acceleration.
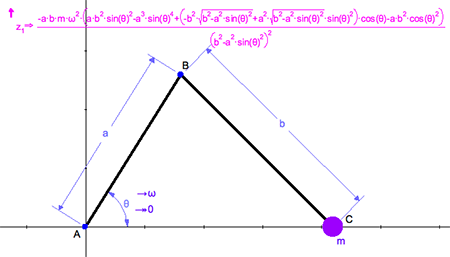
Example - Piston Crank with Mass
A motor rotates AB at constant angular velocity ω. Mass m is attached to point C. We find the reaction force in member BC.
4. Dynamics
Dynamic examples compute acceleration as a result of unbalanced forces.
Inputs are force elements and velocity/acceleration elements. Outputs are accelerations of constraints that are considered free to accelerate.
Example - A Physical Toy
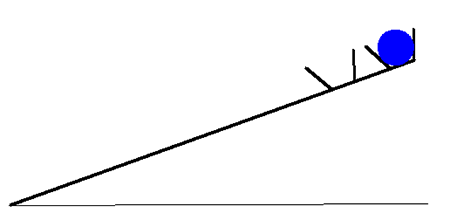
A physics demonstration consists of a wooden bar with two small cups on the end. In the outer cup is a ball. The bar is supported at about 20 degrees to horizontal. When the support is removed, the bar drops to horizontal, and the ball jumps from the outer to the inner cup. How does this work?
First we model the bar by putting a mass m at its center and giving it a moment of inertia of m*L^2/12 (moment of inertia about the center of mass of a uniform bar).
Making angle θ free to accelerate, we can then measure the resultant acceleration of point B.
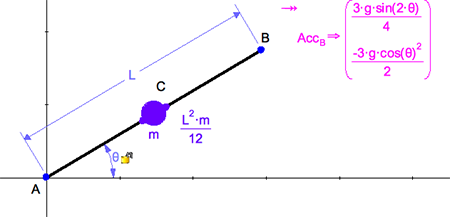
We see that the vertical acceleration is 3cos(θ)2/2 * g. Hence the toy will work so long as cos(θ)2>2/3, or θ<35º.
Many more examples can be found on the Mechanical Expressions website and in the .Doc and .Examples directories of the program installation.
|