Pendulum Clock
Have you ever studied an old pendulum clock and wondered what the pendulum does, and what the purpose of the weight is that hangs behind the pendulum? By connecting standard components from the Mechanics Modelica library using SystemModeler’s drag-and-drop functionality, you can create your own model of a pendulum clock and study the inner workings for yourself.
Para ejecutar este ejemplo necesitará
Las versiones más recientes de System Modeler y Mathematica.
Por favor haga una selección:
Obtener unaprueba gratuita Continuar
con la descarga
The Principles of a Pendulum Clock
The swinging motion of the pendulum pushes on a fork, which releases an escapement wheel that is attached to a counterweight. When the wheel is released, gravity pulls the counterweight down, and the wheel starts to turn. The cogs on the wheel serve two purposes. First, they lock the wheel in place. Second, they are at an angle in relation to the fork face, so when the fork releases the wheel, part of the energy supplied from the counterweight is transferred to the pendulum. Without this, the pendulum would gradually lose energy and quickly become inaccurate.

A typical pendulum clock.

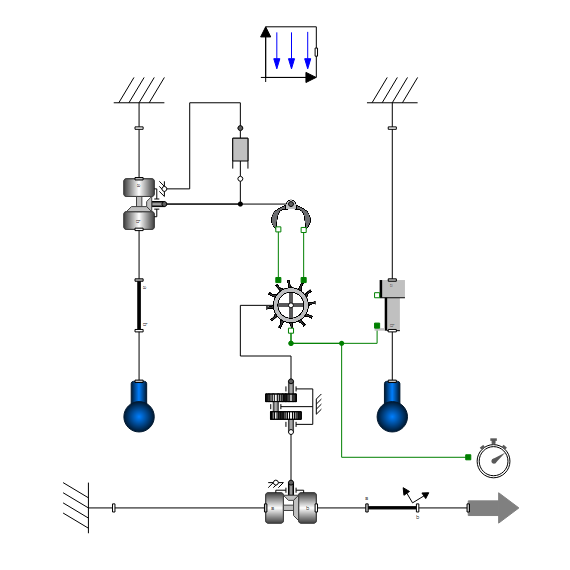
The inner mechanics of a pendulum clock. Three different-sized gears are used to scale the rotational movement between seconds, minutes, and hours. The topmost gear is the escapement wheel.
The Model
The two multibody objects to the left and right describe the pendulum motion and the counterweight, respectively. The pendulum swing is affected by friction, and the energy lost is supplied by the counterweight. The lowest portion of the diagram shows the clock hand. Download the model and see instructions for how you can add a second clock hand.
Analysis
Analyze with the Wolfram Language
Create custom plots, calculate performance measures, and perform parameter sweeps with the Wolfram Language.
For an ideal pendulum without friction, only the length of the pendulum axis determines the length of one period. With friction, however, the length of the period will decrease over time as energy is lost to friction. Now, the mass of the pendulum is important, as this determines the initial energy of the system. The magnitude of the energy supplied to the system is determined by the mass of the counterweight and the angle of the cogs on the escapement wheel. All these parameters need to be balanced so that net energy is kept constant. Even small variations will lead to the clock rapidly becoming inaccurate.
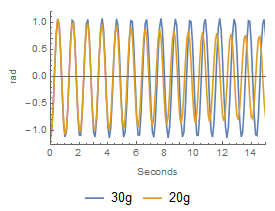
A balanced system, here with a counterweight mass of 30 grams (blue) will keep swinging at a constant amplitude and phase over time. A lower mass will lead to the frequency and amplitude rapidly declining.
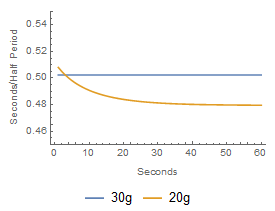
Here the difference between the balanced and the unbalanced systems accumulates to 3456 seconds, or just under an hour, during the course of a day.
Multibody Animation
Using the Modelica MultiBody library, models used can be directly visualized in an automatic 3D animation. This can be used to study the relationship among the swinging motion, the falling counterweight, and the ticking clock hand.
An automatically generated multibody animation.
Wolfram System Modeler
Probar
Comprar
System Modeler está disponible en inglés
y japonés
para Windows, macOS y Linux »
¿Preguntas? ¿Comentarios? Contacte a un experto de Wolfram »